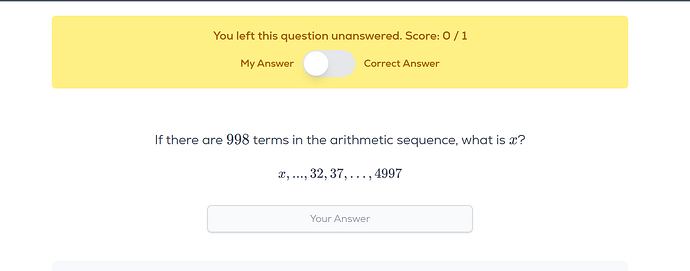
Can someone explain how to do this problem? The solution video used the sum of multiple method to solve this problem. However, the multiple that was used is 5, which is not a multiple of the last or first number.
The multiple you use is more about the spacing between each item, rather than the start/finish:
For example:
3, 8, 13, 18, 23
In this sequence, you can see the numbers are 5 apart, even though the start and finish are not multiples of 5.
If we do \frac{23-3}{5} + 1 we get 5 which is the number of terms here.
Does that make sense?
It does make sense however, in the lesson for finding multiples in a set of numbers; the formula states to use the last multiple and the first multiple in a set. Is this not necessary based on what you said?
This is a different problem though.
We’re not finding:
How many multiples of 5 are between the first and last term
We’re finding
How many times can we split the distance between the first and last term into fives (the interval between each item)
In this example:
3, 8, 13, 18, 23
The actual multiples of 5 are 5, 10, 15, 20 which is 4