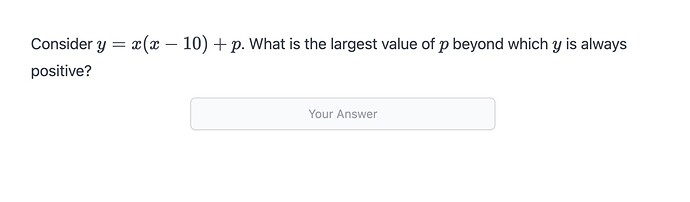
Why the largest value of p should 25, ill choose p as 26 (larger than 25), and y will be positive (Always).
So would 25.01.
So technically 25 should be smallest number rather than largest, right? The D thing making it counter intuitive, can you explain the discrepancy, please?
25 cannot be the smallest number because any number less than 25 would also not satisfy the condition “y is not positive”.
Oh! what i meant, that 25 would be the smallest number to make the y “non negative” always, and anything >25 would make y +ve, always, in every case.
Correct, but then notice the words “beyond which” in the question.
Oh! understood, thanks. Just one thing, if we change the word smallest instead of largest, would it change anything?
Like : What is the smallest value of p beyond which y is always positive?
This is what making me jittery.
- “smallest value of p beyond which” doesn’t make sense.
- “smallest value of p for which y is always positive” is technically 25 + \epsilon, where \epsilon is greater than 0. This is used to indicate that any positive value greater than 25 (even if it is 25.0000001) would work. This is not something you can input in the textbox however.
- “smallest value of p for which y is non-negative” would be 25 though.