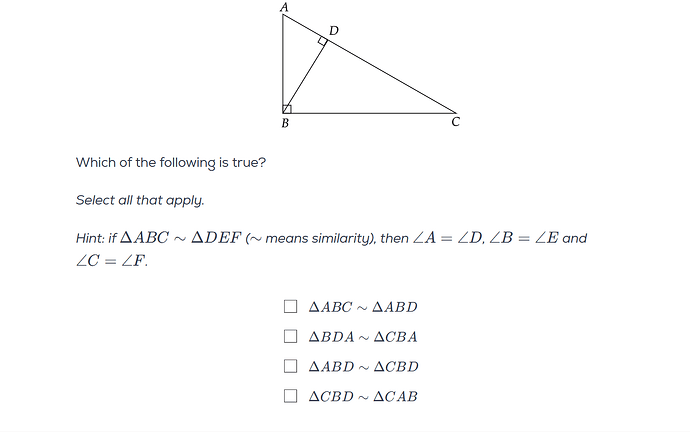Hi, do the notes below help? You need to rotate the triangles in a way so they are oriented the same. Then you need to ensure the angles are the same in the order presented.
Does that help you?
Thanks Ganesh. So essentially we should be looking at the position of the 90 angles in both the triangles? And as long as they are in the same position, we consider the two triangles similar? Or do we look for at least two of the angles to be same?
Asking because nothing is mentioned about the remaining two angles… even though Greg solved it by assuming they were all 30-60-90 triangles. But I don’t see anything in the question to indicate these are 30-60-90
another question pertinent to such problems: when we draw a perpendicular (such as from B to point D) won’t it intersect the angle at B into two equal halves? Thereby making each angle at pt B 45 degrees?
Let \angle A = x then find \angle ABD and \angle C in terms of x.
Now order the vertices of the two triangles concerned in such a way that all the angles match.
\overline{BD} is an angle bisector (and passes through the midpoint of only \overline{AC}) if \overline{AB} = \overline{BC}, which would imply a 45-45-90 triangle in this case. Needless to say, you’re not provided any information that this is a 45-45-90 triangle, so such an assumption is unfounded.
In general, \overline{BD} is an angle bisector iff \frac{\overline{AB}}{\overline{BC}} = \frac{\overline{AD}}{\overline{DC}}
Thanks a ton! Sometimes I just get stuck on the most basic of concepts for some weird reason that I just can’t fathom!