Ah okay, I think I get it. So 3^31 would have a remainder of 3, and 3^107 would have a remainder of 4. Is that right?

how is the answer 3 here ? I know the unit digit of 3^33 is 3. But I do not know what will happen when that whole number gets divided by 10.
Those two sentences don’t support each other. If you know the unit digit is something then you know what the remainder is when you divide an integer by 10.
I think I understand what you’re asking. We know 10 is greater than 3, so you are trying to determine what the remainder would be since 10 does not divide into 3, right?
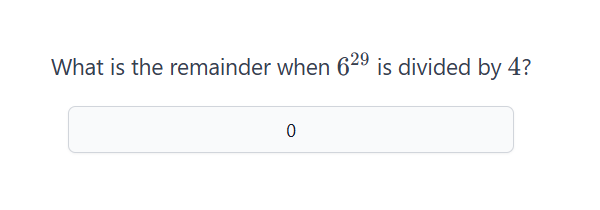
For this problem, we know that 6^4 will follow the same rule as 6^28 right? So why doesn’t 6^29 follow the same rule as 6^1 / 6^5 / 6^9 , etc…?
6^{29} leaves the same remainder as 2^{29} when divided by 4, and maybe that’s more approachable for you?
Uhhhh 6 = 2 \cdot 3 and so 6^2 = 2^2 \cdot 3^2. You should be able to see that any integer powers greater than or equal to 2 can be expressed as a multiple or 4 (Why?).
Thus 6^n for n \geq 2 leaves a remainder of 0 when divided by 4.
That makes sense! Another question for you though…
In the above example that I posted used 3^n/7, you mentioned using positions to extrapolate larger exponents. When would I use positions as mentioned above, vs using the method you explained in your last example.
3^n for reasonable n can never contain a 7 in its prime factorization. Thus my previous “method” doesn’t make sense. Hopefully, you can see how this is different from the remainder of 6^n when divided by 4
Essentially, the “pattern” thing works if the base of the numerator and denominator are both coprime. For example, 3 and 7 are coprime; however, 6 and 4 weren’t.
That makes sense. Thank you so much for the help!