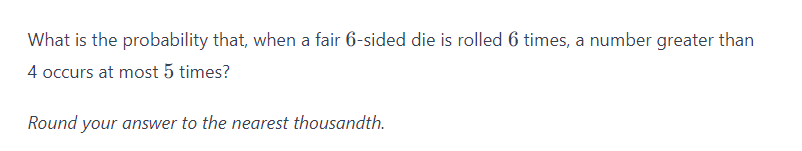Rolling a die 3 times, what's the probability of getting all 3 5s or all 3 6s?

GRE Quant Problem Solving
1

Hi friends,

To solve this problem, I think the way should be:

  • Probability of getting 3 5s are (1/6)^3

  • Probability of getting 3 6s are (1/6)^3

So, the answer is: (1/6)^3 + (1/6)^3 = 2/6^3

However, in videos, the tutors guide that:

  • Probability of getting 5 or 6 in one time is 1/3. Because we have 3 rolls, the probability of getting all 3 5s or all 3 6s is (1/3)^3

Could you please explain to me where I am wrong?

Thank you so much.

2

Where is this from? Can you share a screenshot?

3

Please check out the blue-colour part in the screenshot. It explains how to calculate the probability of getting 5 or 6 six times in 6 rolls.

It is from Question 2, At LEAST/MOST Questions Exercise.

Another example can be found in question 14/24, PrepSwift Quant Tickbox Quiz #15 (Data Analysis Column 3).

Thank you.

abc
abc768×486 15.5 KB

4

Regarding the blue colored in the screenshot, I think the answer should be:

  • Probability of getting 6 5s are (1/6)^6
  • Probability of getting 6 6s are (1/6)^6

So, the answer is: (1/6)^6 + (1/6)^6 = 2/6^6

Not (1/3)^6.

Thankyou.

5

Can you share a screenshot of the question itself?

6

question
question802×151 5.04 KB

Here it is, please

7

The problem is that you’ve “converted” the problem incorrectly. “5 or 6 three times each” is not the same as saying “greater than four six times”.

8

Oh yes, it was my bad.

Thank you so much Leaderboard!