X(x+3)(x-5)>0

[C.Koushik]

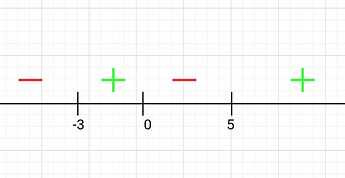
If you get an equation like a.b.c.d > 0 (or a.b.c.d < 0), all you gotta do is draw a number line. Mark all the points where the terms a, b, c, and d are zero. And mark the alternative regions + and -, and pick the regions you want.

For your question, the roots would be x=0,-3 and 5

1. Draw a number line and plot the zeroes like this
   
   
2. Select a point in any region, and find what the value of the expression will be.
   
   
   
   For instance, I chose 8 here. So The value of the expression will be 8(11)(3) = +264. So any number in the region (5, \infty) will give us a positive value for the expression. So mark the region as +ve.
3. Mark the other regions alternately with + and -
   
   
4. Now, from the question, you want regions where the value is +ve, so your answer is (-3,0) and (5,\infty)

NOTE: One exception for this method is when you have the same term repeated an even number of times, say x(x+3)^{2}(x+5). In that case, the equality does not switch to the opposite sign about the point -3