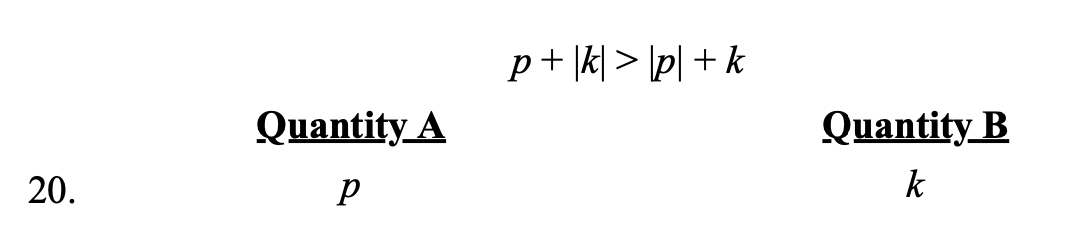p -|p| > k -|k| which tell us that p is positive and k is negative. So A
could you explain with an example?
Don’t worry, his reasoning is wrong. Could you show your attempt instead?
As a hint, consider the definition of an absolute value function:
|x| = \begin{cases}x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases}
Now consider 4 cases in tandem with the above definition:
-
p \geq 0 and k \geq 0
-
p \geq 0 and k < 0
-
p < 0 and k \geq 0
-
p < 0 and k < 0
Why it is wrong? can’t we rearrange the inequality?
Why is it wrong?
Let p = -3 and k = -5, then you have that -6 > -10, which is a true statement. Clearly, p isn’t positive as you mentioned above.
Can’t we rearrange inequality
Yes you can, but your implied conclusion after doing that wasn’t right.