Algebra Foundation Quiz #1 (Question 14 and 17)

[Archi]

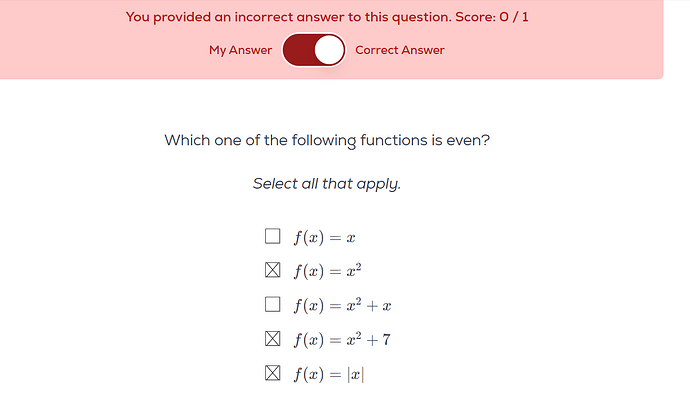
For even function question, I am confused why option 1 is not correct. The answer key shows that only 2nd and 4th are correct. My reasoning for choosing 1st was it will always give us positive value which is one of the main conditions for even function but there are other conditions too such as all degree should be even and in this case it is not which means it is also not symmetrical about Y axis so my question is would we always check for both these conditions to get fulfilled - all degree even and f(-x) = f(x) so, does both need to strictly be true at the same time?

Does that mean absolute value cannot have any overpowering implication over it?
For eg - If we have two functions:
A. -|x^2| : would you consider this as even function or not?
B. |x| : Would you consider this as even function?

In both the examples A and B only one condition is being fulfilled. I would be grateful for any guidance on this because in Prepswift Quant Tickbox quiz#6 (Algebra Column 3) answer key showed otherwise. I have attached the screenshot below for this. You will notice that answer key considers |x| as even although it has an odd degree.

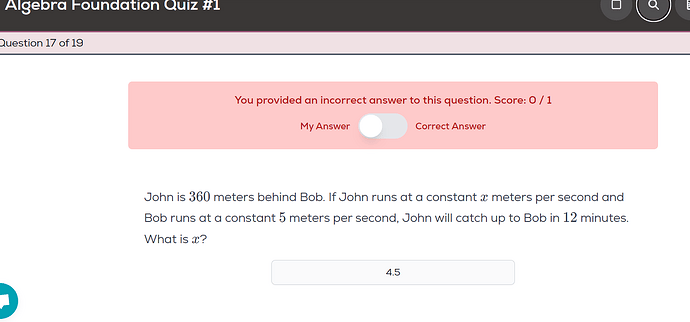
For last question, I want to ask why is answer not 4.5 because in the previous quizzes we have assumed the other person to be in rets position and then used the formula of relative speed so in this case-

D = RT
360 = (5-x)12*60
x= 4.5

The answer key shows - 5.5 so according to me 5.5 can only come when but previously in most of the solution videos these questions have solved by taking into the account the distance that person is behind or am I misremembering something -

Convert 12 minutes to seconds:12 minutes=12×60=720 seconds

Calculate the distance Bob runs in 720 seconds: Since Bob runs at a speed of 5 meters per second:Distance Bob runs=5 m/s×720 s=3600 meters

Calculate the total distance John must cover: John starts 360 meters behind Bob. Therefore, to catch up, John must run the distance Bob runs plus the initial gap:Total distance John runs=3600 meters+360 meters=3960 meters

Set up the equation for John’s speed: John runs this distance in the same time (720 seconds):Distance=Speed×Time → 3960=x×720

Solve for x:x=3960/720 → 5.5 m/s

For eg- Refer to this explanation video in overwhelmed study plan for relative speed we haven’t added distances here so why in this question. What is different about it?

[Leaderboard]

In the future: one question per post.

---

@Archi

it will always give us positive value which is one of the main conditions for even function

This is incorrect. Recall that the definition of an even function is f(-x) = f(x). Nothing stops f(x) from being negative.

This is also not a polynomial, so either (i) work from the definition or (ii) choose numbers.

@Archi

For eg - If we have two functions:
A. -|x^2| : would you consider this as even function or not?
B. |x| : Would you consider this as even function?

But are even. Also: -|x^2| = -(x^2).

@Archi

You will notice that answer key considers |x| as even although it has an odd degree.

Again, |x| is not a polynomial.

@Archi

D = RT
360 = (5-x)12*60
x= 4.5

John is faster than Bob.

[Archi]

Yeah sorry. I will make sure to not ask more than 1 question in one post. I understood the answer for relative speed but the question doesn’t explicitly mention that John is faster than Bob so what indicators can we look for to arrive at that conclusion. Is knowing that John will catch up to Bob only when he is faster enough of an indicator @Leaderboard ?

Another question for even function question:

1. I am still not clear if we should look for both the indicators to be true at the same time- i.e. even degree and f(-x) = f(x)

2. In your answer “This is incorrect. Recall that the definition of an even function is f(-x) = f(x). Nothing stops f(x) from being negative.” how does it matter what number we choose because answer would still be a positive number like if f(-4) then |-4+2| is also positive. Like how is this case different from |x| which is considered as even function ?

3. I wanted more clarification on this, “This is also not a polynomial, so either (i) work from the definition or (ii) choose numbers.” Does that mean any function inside an absolute value is not a polynomial?

[Archi]

Do you mean to say that we need to substitute values like this?

[Leaderboard]

@Archi

Is knowing that John will catch up to Bob only when he is faster enough of an indicator

Yes.

@Archi

• I am still not clear if we should look for both the indicators to be true at the same time- i.e. even degree and f(-x) = f(x)

If it’s a polynomial, pick one; f(-x) = f(x) will always work though.

@Archi

answer would still be a positive number

which is not needed. And |x + 2| is not even because f(4) \neq f(-4) for instance.

@Archi

Does that mean any function inside an absolute value is not a polynomial

Yes.

@Archi

Do you mean to say that we need to substitute values like this?

Yes, or try some values.

[Archi]

Thank you for being so patient. I understood it now!