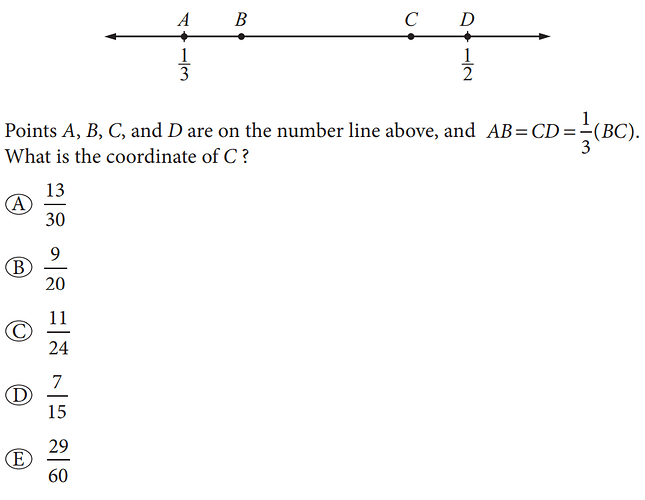n is the dividend right and 45 is the divisor then how do I find a divisor
Based on the length how do i get the coordinates
How do I apply the same for thw squares?
How do I calculate for A(200) after 101
Have you made any effort to search the questions on the internet?
Yes I did
1.For the first one I wanted to know whats incorrect in my understanding
2. I got this as the soln
Assume Length of AB = x
so AB = CD = x and BC = 3x
so distance between AD = 5x=13−12=165x=13−12=16
or x=130x=130
now AC = 4x+13=430+13=1430or715
3. For the third one I didnt follow the absolute and squaring relation
4. For the last one they did A(100) + (101)
but post 101 they did some simplification which I didnt follow
Just take n = 18. Only 9 and 6 are divisors of 18.
Now take (18 + 45) = 63. Only 9 is a divisor → that’s the answer.
To solve it formally, notice that \frac{n - 18}{45} is equal to an integer. Call it k. Write n in terms of k and factorise.
Indeed, you have -1 \leq z \leq 1. The square of both negative and positive numbers is positive, which means that z^2 \leq 1.
B and C are easy to disprove by taking a negative value of z.
Probably did
A(200) = A(100) + (101 + 102 + … + 200)
A(200) = A(100) + (100 + 1 + 100 + 2 + 100 + 3 + … + 100 + 100)
A(200) = A(100) + 100 × 100 + (1 + 2 + 3 + … + 100)
A(200) = 5050 + 10000 + 5050
A(200) = 20100
for 4
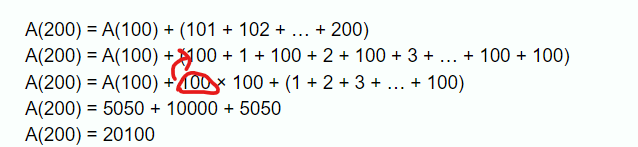
That 100 is from there right
Thanks for answering my remaining queries
Indeed - 100 is added 100 times.
Yes (that is, AC = AB + BC)