Arithmetic Problems

GRE Quant Problem Solving
1

Hi y’all, I am reviewing my foundational knowledge of arithmetic, and need help to solution on the following arithmetic problems:

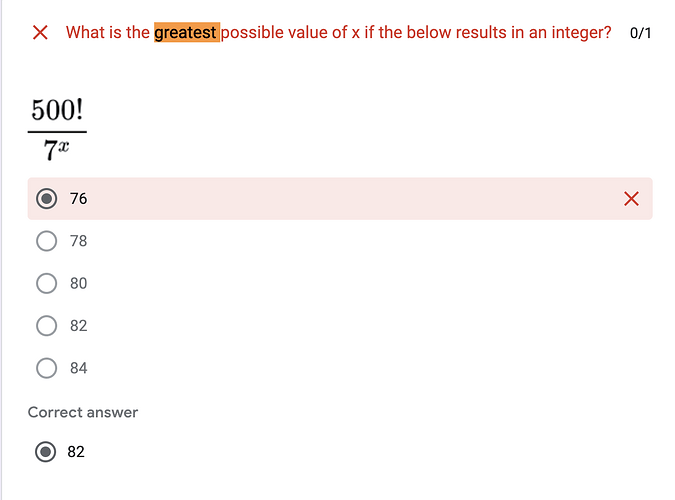
  1. What is the greatest possible value of x if the 500!/7^x results in an integer?
  2. How many trailing zeros does 500! have when 500! is written as an integer?
  3. What’s the unit digit of 2^30 + 3^30?
  4. How many positive factors and positive even factors does the number 337,500 have? My answer was 13 because when add +1 to the exponents you get 6+3+4. did I miss a a prime factor. And I am lost how to find even factors.
  5. If |x-3|=5, then the product of the two possible x values is what number? -16 is the correct answer, I got -14. how did they get -16?
  6. In a fruit basket containing only apples and oranges, the ratio of apples to oranges is 3:8. If the basket contains more than 40 pieces of fruit, what is the minimum possible number of apples?
  7. Yesterday, the ratio of dogs to cats was 4:7. Today, the ratio of dogs to cats is 5:6. The ratio today is what percent larger than the ratio yesterday?
  8. What is the remainder of -21/4? How is the remainder equal to 3?
  9. What is the greatest possible value of x if 50!/4^x results in an integer, if x is an integer?
  10. What is 700% more than 2 equal to?

Any assistance is greatly appreciated, thank you!

2

I mean since you posted a bunch of questions then i guess we should start one by one.

What’s your idea to solve this?

3

Hi, for this one, it was a MC question and was approaching it with PF of 500, but realized there aren’t any 7’s when you factor it, so then went to 490 which is a a multiple of 7 and 7^2 * 10, therefore x = 49; but the correct answer was 82 so I’m confused on how they came to that answer?

4

It’s 50! and not 50, which is why you can see that the answer is quite “big”.

5

Screen Shot 2024-11-25 at 10.35.16 PM
Screen Shot 2024-11-25 at 10.35.16 PM1276×944 42.3 KB

here’s the problem and how diid you come to that conclusion?

6

I didn’t come to any conclusion. I’m saying it’s 500! and not 500 (u prime factorized 500).

Oh yeah, i made a typo with the 50, but my point should’ve came across regardless.

7

Locking this. @user2009, please put one question in one thread, and follow How to Ask Better GRE Questions on Forums when doing so.