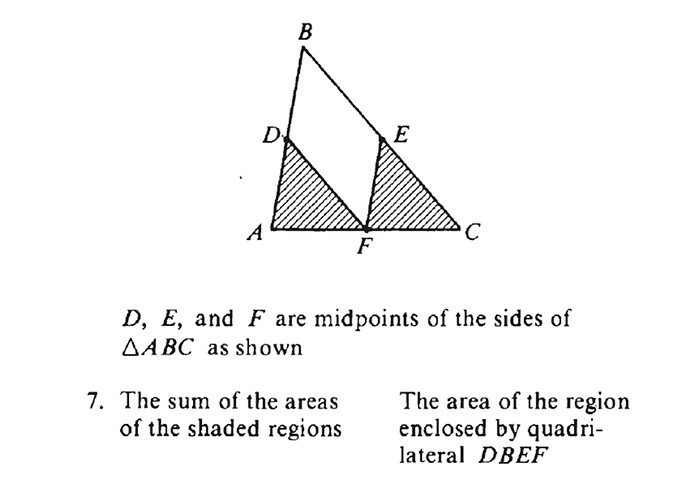
Can anyone please explain mathematically why the perpendicular (height) from B to DE would be the same as from D to AF?
Show that \triangle BDE \sim \triangle ABC and that should be sufficient to answer your question
They are similar, but I thought that only signalled proportionality of the sides. Would it be the case for perpendiculars also?
Yes. If you’re not convinced then you can show that it is the case.
Let the foot of the altitude in \triangle BDE be denoted as H and the foot of the altitude
in \triangle BAC as N. Now you have that \triangle BDH \sim \triangle BAN by AA or whatever u like. Thus the heights are in the same ratio as the corresponding sides.
I guess this question is better solved by realizing that \triangle DEF is a medial triangle and then usual shenanigans should already tell you that the 4 triangles are congruent.