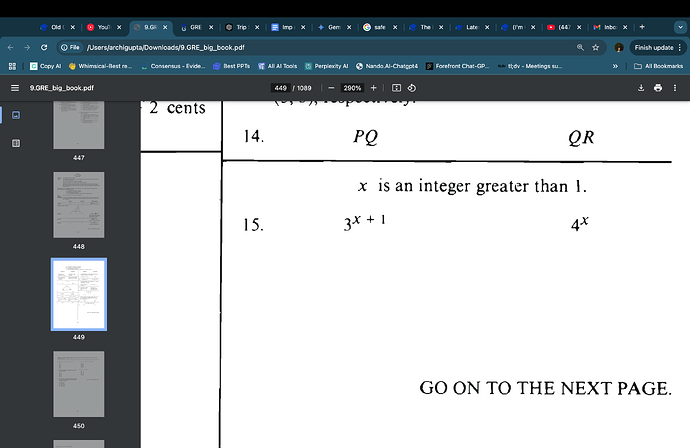
Hi, this is a QC question. My answer for this is B because it is always increasing by higher factor as compared to A and since x is an integer greater than 1 there is no such case that could dispute this generalization. The answer key shows D but I am unable to find a case that would reject this claim. i would be grateful for any help in understanding where am I going wrong?
x = 2
3^3 = 27
4^2 = 16
A>B
x = 4
3^5 = 243
4^4 = 256
B>A
Please see these examples. An interesting way (optional) you might think about this is observing that A>B for the first few integers, but think about a limit as x → infinity. then, the 2 exponents kind of approach the same number, at which point B > A.
Im not sure this is 100% rigorous, but you should just be extra wary with questions like these to check for the possibility of D being the answer.
Hi thank you so much. You made it look quite easy now. I should have tried more examples. I think I just made calculation mistakes. ![]()
Alternatively, you can divide both quantities by 3^x and then you’re essentially comparing 3 with (\frac 43)^x. This is fine cuz 3^x is always positive and so the inequality (comparison between two quantities) is preserved.
That is a nice suggestion. Thank you very much ![]()