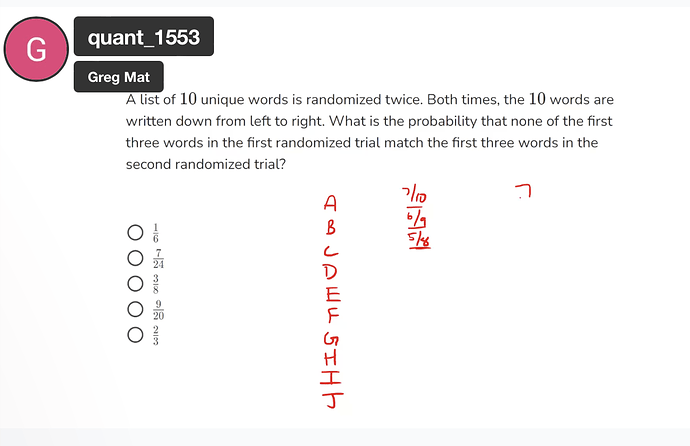
My calculation was, on a second randomized trial, the probability of A not being placed in the first “A”'s place is 9/10(excluding A) and the prob. of B not being in the first B’s place is 8/9 and the prob. of C not being in the first C’s place is 7/8. So multiply three probabilities and it will come out as 7/10.
But the greg’s video says 7/10 times 6/9 times 5/8 (total 7/24). Can anyone explain this? Thanks:)
It’s because the question ask that None of the first 3 words in Randomized 1st should match the first 3 words in randomized 2nd
I still don’t get it. Doesn’t that mean, in the second trial, the probability of the first word not matching the first trial word(A) is 9/10? because the second trial “A” should not take place?
it’s none of the first three words in the question and not the first word only which ur thinking.
Let me make it easy for u :
\text{ Let letter be :}
\begin{aligned}
A \\B\\C\\D\\E\\F\\G\\H\\I\\J\\
\end{aligned}
Now, when we come to second randomized our letter choice can’t be : A,B,C due to the criteria “none of the the first three words in the first randomized trial match the first three words in the second randomized trial” thus, Our first word can’t match either A or B or C \rightarrow \dfrac{7}{10} Choices and you’re thinking that it can’t only match A thus, you’re doing \dfrac{9}{10} Choices which is not the case!
Oh, I got it now. Thanks!!
Nice!