The answer is 3. The 21/2 is 1.414 and also 41/4 is the same, which indicates that there is a maximum value in between 2 and 4. clearly the question asks us for the integer and that is one and only 3.
If you want the exact value that would be ‘e’(2.71 around), which can be obtained by maximizing the function y=b1/b
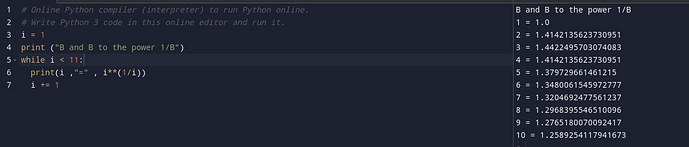
I tried my best to solve logically but I failed. I believe it has to do something with number and its properties along with concept of roots. Anyhow I ended of writing a script and got the answer to be 3
thank you I was wondering there had to be a logical way to solve this.
Let b be an integer from 1 to 10, inclusive. For what value of b is b(1/b) is at its maximum point?
I am going to assume that y = b(1/b) will have some kind of trend where y will increase at first and then start decreasing
when b = 1, y = 1(1/1) = 1
when b = 2, y = 2(1/2) = 1.4 (increase)
for b = 3
I calculate 1.4 x 1.4 x 1.4 = 2.744
So the value of y when b = 3, has to be greater than that of b = 2 (increase)
when b = 4, y = 4(1/4) = 2(2/4) = 2(1/2) = 1.4 (decrease)
Going by my initial logic, the answer should be 3
Not sure if this is the best solution out there
so is it done by trying numbers?
That would be a reasonable approach indeed.
I verified your answer by blotting the graph on Wolfram Alpha.
How would you plug in 21/2 on the GRE calculator? or is that a number that you know without calculation?
I do not understand where you got 1.4 x 1.4 x 1.4 … that seems to me to be 21/2 x 21/2 x 21/2 which is not the same as 31/3, which is what the question is asking for? Or are you simply using it as a comparison method?
I think it’s a comparison method. Here’s how. You start with 2^{\frac{1}{2}} and 3^{\frac{1}{3}}. Then cube both sides. This leaves you with 2^{\frac{3}{2}} and 3. For the former, what she did is rewrite it as {(\sqrt{2}})^3 and estimated \sqrt{2} as 1.4, with 1.4^3 < 3. (it could be 1.414 for a bit more precision, but that is not necessary here)
A even stronger way would be to raise them to a power of 6 instead. That gets to 23 and 32, and it’s easy to show that 8 < 9, with no estimation required.
I have memorized the value, but you can do this on a GRE calculator as well
A comparison method. I think @Leaderboard explained it well.
Ans is 3