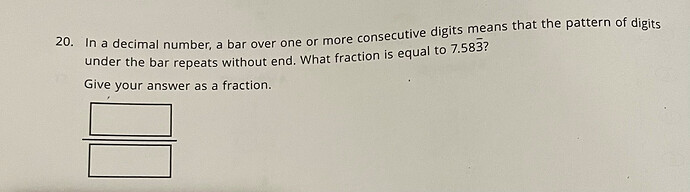I tried to convert the decimal to fraction with Greg’s method, but my result is a big fraction. I am having a difficult time simplifying it also. The book solves it in a different way which is confusing to me. Hope anyone can help.
This is a quite interesting problem. So we know that we use the decimal system. Then, the number 7.58\bar{3} can be expressed as 7+0.5+0.08+0.00\bar{3} (because decimal system, right?). It should seem fair to say that the most difficult part will be to deal with the 0.00\bar{3}, but let’s go through it all step by step. So now that we decomposed our number in such way, let’s switch to fractions. Recall that the decimal system implies playing with integer exponents of 10. Then 0.5=5\cdot 10^{-1}, 0.08=8\cdot 10^{-2}, and just for the sake of this representation, 0.00\bar{3}=\bar{3}\cdot 10^{-3}. Let’s add up the first two numbers, and the 7 also, so we would have \frac{758}{100} and we still need to deal with our tedious 0.00\bar{3}. One key is to notice that \frac{1}{3}=0.\bar{3}. Why is this important? Becuase we have a “base” we want to transform, that is, if we know that \frac{1}{3}=0.\bar{3}, but we need 0.00\bar{3}, what can we do to the former number in order for it to look like the second number? What would happen if we divide 1/3 by 100? We would get that \frac{1}{3}\frac{1}{100} = 0.00\bar{3}. This is the hardest part of the problem. Now just combine the two fractions we have already derived: \frac{758}{100}+\frac{1}{3}\cdot\frac{1}{100}, which is then equal to \frac{2275}{300}. Whether you want to simplify or not that’s your choice, but just plug in this number in your calculator and you’ll see that this fraction works!
The back of the book gives the answer 19/12, which I was a bit confused thinking that has to be the only answer. So, the idea is that if I get a different fraction than what the book states and plug it in the calculator. The result should equal 7.5833333…?
First, 19/12=1.58333333… so that’s already wrong, but this is probably a typo, because the fraction we got is way too big. Anyhow, the GRE allows for equivalent fractions, so no problem if it is 2275/300 or 455/60