Questions:
Eight points are equally spaced on a circle. If 3 of the 8 points are to be selected at random, what is the probability that a triangle having the 3 points chosen as vertices will be a right triangle?
Doubt:
I watched Gregmats video on the choice method used to solve the question in the screenshot
I understand why we do $1 \times 3/7 \times 2/6 \times 1/5 in this question and I tried applying the same logic to the question on right triangles as follows:
-
Probability of picking the first point out of 8 points = 8/8 (since we dont care what the first point is)
-
Probability of picking the second point given that this point must be diagonally opposite the first point for the line to to form a right triangle = 1/7 (ie only one point of the remaining 7 is diagonally opposite)
-
Probability of picking the third point (doesnt matter since any other point picked will form a right triangle)
Hence probability = (8/8)\times(1/7)\times(6/6) = 1/7
However, the correct answer is 3/7.
Please help me understand what is wrong.
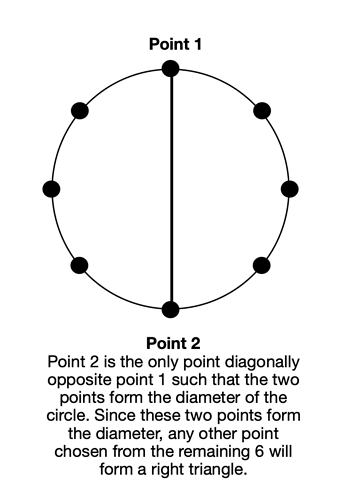
Can you sketch an example for point 2?
Here is a screenshot.
For point 2, I am relying on the property that to form a right triangle within a circle the two points should be opposite each other such that they form the diameter of the circle.
You’re approaching this using permutations (i.e, where the order does matter). I think the problem is that you have not considered the different rearrangements for the third point of the triangle.
Hi,
I tried solving it keeping your tip in mind but am still not able to figure out. Could you please elaborate on what you mean or share a solution?
Thank you for your time, greatly appreciate the help.
There are two ways to look at this. The one I did is to assume that the order of the vertices does not matter.
First: how many triangles can we create amongst 8 points? That’s \binom{8}{3} = 56 ways.
Now: let’s build a right-angled triangle. Taking your logic, find the number of distinct “diagonal” lines with two points. Notice that there are only four ways - after all, line AB is the same as line BA.
Finally: where can we put the third point? Again following your logic, we can put it in any of the remaining 6 vertices. This means that the total probability would be
\frac{4 \times 6}{56} = \frac{3}{7}
Coming back to your solution: what you did is work with permutations instead (i.e, assuming that the order matters). This means that you somehow need to account for the 3! = 6 ways you can arrange the vertices of the triangle in the last step. You did this partially by accounting for the different ways of arranging the vertices in the line (as you did not assume that line AB and BA are the same), but this made it harder for you to handle the last step, where you needed to consider the different ways of arranging the last point as well in the triangle (which would require you to multiply by 3).