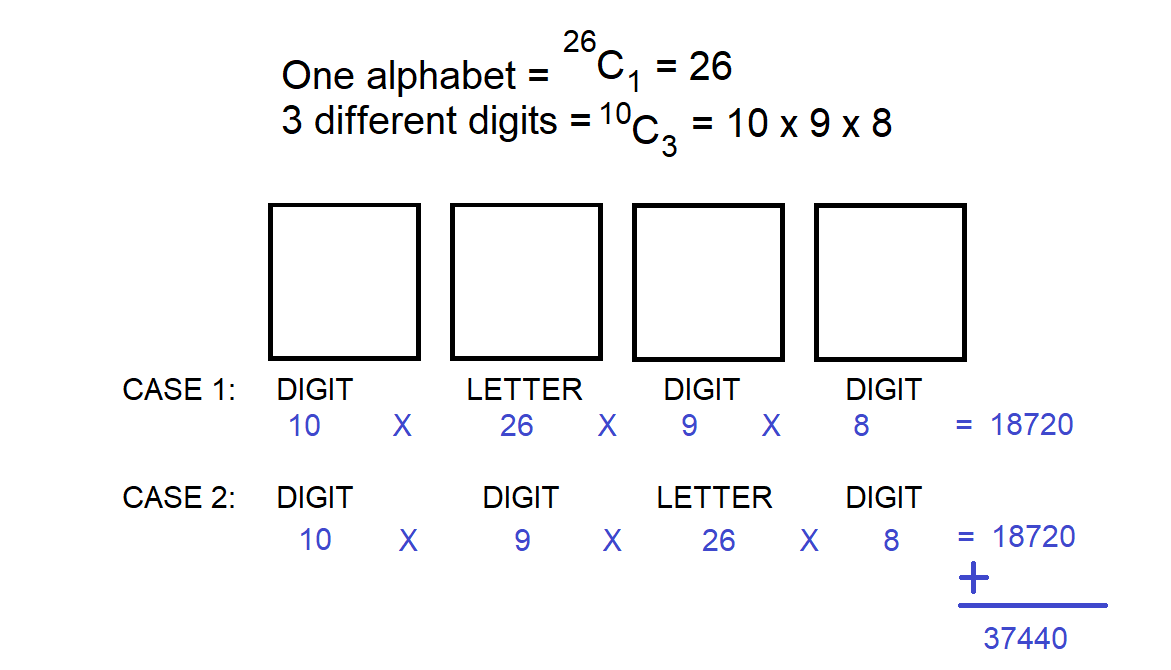
A four character password consists of one letter of the alphabet and three different digits between 0 and 9 inclusive. The letter must appear as the second or third character of the password. How many different different password are possible?
a. 5040 b.18720 c.26000 d.37440 e. 52000
E. 52,000
I solve it based on number of possibility each letter or digit can be inserted.
If the letter in the 2nd digit: 10 X 26 X 10 X 10 = 26,000 possibilities
If the letter in the 3rd digit: 10 X 10 X 26 X 10 = 26,000 possibilities
Add them up = 26,000 + 26,000 = 52,000 (E)
Since the question mentioned “Three different digits” we should reduce the number of digits:
If the letter in the 2nd digit: 10 X 26 X 9 X 8 = 18,720 possibilities
If the letter in the 3rd digit: 10 X 9 X 26 X 8 = 18,720 possibilities
Add them up = 18,720 + 18,720 = 37,440(D)
I did this in the same way but the answer is 37440
so.
The answer is 37400
2261098
“2” means that the letter can be in the 2nd or the 3rd position
“26” means that there have 26 different letters can be choosed
1098 comes from the phrase “three different digits”, as it indicates that the remained three positions should be put into three different digits. Thus, the first position gets ten choices, leading the second has 9 choices, and lastly, the final empty position only gets 8 choices.
So that the equation is 1098
2261098 = 37400