Hi @gregmat,
I have tried to include lacuna in approach mentioned in today’s class and also detail explanation for solution other than Brute Force… Please let me know…
NOTE: When we were using 3/4 * 2/3 * 1/2 * 1/1 = 6/24 You were missing some cases because…
- At first place 3 letters can come… True… B,C,D… But that does not mean that at second place only 2 letters can come… If B is used in first place then A,C,D all can come in second place hence we were missing some cases…
- Similarly Probability for choosing first letter correct is 3/4… True… but choosing second letter correct would not be 2/3… It will be dependent probability on first letter chosen…
- Direct Multiplication will not help here… because Placing B at first place is different than placing C or D at first place… because placing C or D limits choices for second place to 2 (A,C or A,D)… But B does not… as all (A,C,D) can come to second place…
Detailed Solution:
In the above question, we can also use Inclusion Exclusion principle of Sets… From where derangement formula is also derived…
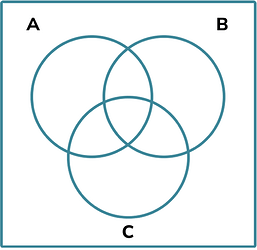
Let’s assume there are 3 Freinds, Adin, Brigid and Chioma only… and below diagram represents,
A = All combinations when A get correct dish…
B = All combinations when B get correct dish…
C = All combinations when C get correct dish…
Then our answer to NO-One get correct dish = n! - Cases(A U B U C) [Here n=3 as A,B,C only]
Using Inclusion exclusion principle we can say… (Please Notice alternate + and -)
Cases(A U B U C)
= [Cases(A) + Cases(B) + Cases(C)] - [Cases(A ∩ B) + Cases(B ∩ C) + Cases(C ∩ A)] + [Cases(A ∩ B ∩ C)]
= Cases(1 person getting correct) - Cases(2 person getting correct) + Cases(3 person getting correct)
As cases of A getting correct food = Cases(A) = (n-1)! (where n=3 (A,B,C) here) (As rest letters can be arranged in (n-1)! ways)
Similarly for B getting correct food and C getting correct food…
or Cases(1 person getting correct) = nC1 * (n-1)! = n!
As cases of A and B getting correct food = Cases(A ∩ B) = (n-2)! (where n=3 (A,B,C) here)
Similarly for other 2 cases of Cases(B ∩ C) + Cases(C ∩ A)…
or Cases(2 person getting correct) = nC2 * (n-2)! = n! / 2!
.
.
.
extending this to k-people getting correct food… nCk * (n-k)! = n! / k!
Now we can say from above inclusion exclusion principle for n people…
Cases(A1 U A2 U A3 U … U An) = (n!/1!) - (n!/2!) + (n!/3!) - … + (-1^(k-1))*(n!/k!) + … + (n!/n!)
hence total cases when no-one get correct food = Total Cases - Either one get Correct Food = n! - Cases(A1 U A2 U A3 U … U An)
= n! - [(n!/1!) - (n!/2!) + (n!/3!) - … + (-1^(k-1))*(n!/k!) + … + (n!/n!)]
= n! [ 1 - (1/1!) + (1/2!) - (1/3!) + … (-1^(k))*(n!/k!) … - (n!/n!)]
which is also called derangement formula…
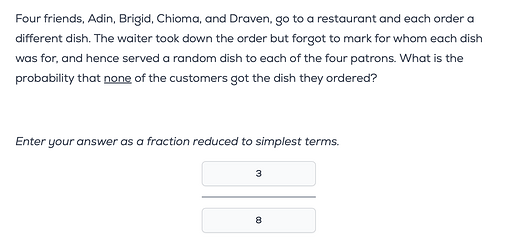
for n = 4 => 4! [ 1 - (1/1!) + (1/2!) - (1/3!) + (1/4!) ] = 24 - 24 + 12 - 4 + 1 = 9 Cases (No-One get correct food)
Resulting answer = 9/24 = 3/8
Please let me know something could be more lucid…
Thank you