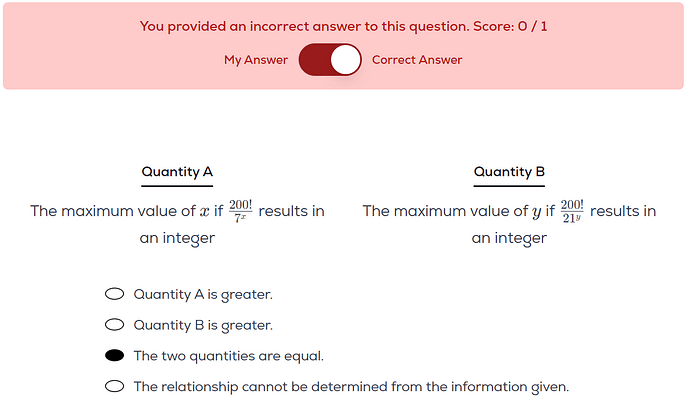
Why is this the correct answer?
It seems obvious that there are more 7s in 200 than 21s, no?
I watched the video that says we should focus only on the limiting factor (in this case, 7 in Quantity B), but still, if we are considering the answer to this question equivalent to “How many 7s / 21s are there in 200”, then it does not make sense to me to say they’re equal??
Why would that be?
200/7= 28 r 4
200/21 = 9 r 11
There are 28 7s while there are 9 21s.
For each 21, there are three 7s. Meaning, there are 3 times as many 7s as there are 21s within any interval. This is illustrated by the calculation I did above, as 28 is almost 3x9.
We literally need three sevens to get only one 21. I am really struggling to see how we can say there as many sevens as 21s.
What about 3? 21 = 7 \times 3, so would we have more 3s or 7s?
By the same logic, I’d say more 3s because each 7 represents two 3s (remainder 1).
I’m really thinking of this in terms of building blocks. For example, if I have a restaurant with meals consisting each of 2 sandwiches and 1 drink, then the restaurant definitely has more sandwiches than drinks. We also have more sandwiches than meals, as 2 sandwiches are necessary to make up a meal.
Correct. However, we need the number to both be divisible by 7s and 3s. Since we have fewer 7s, that’s the limiting factor.
Correct, and suppose you have 10 sandwiches and 6 drinks. What’s the limiting factor? It’s sandwiches (because we have only five pairs of them) - with a drink left over. Same here - the 3s are left over.
Hmmm, I think I got that. Thank you!