Hi,
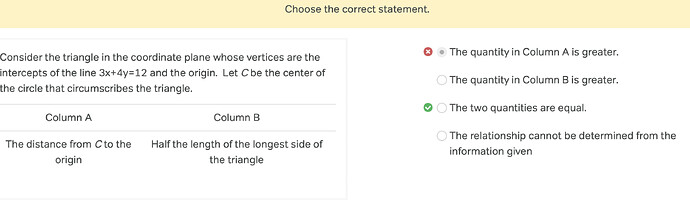
This question doesn’t specify that point C (center of the circle) is on the largest side of the triangle, presenting two cases as shown in the figure: one where C (in blue) is on the hypotenuse and another where C (in red) is outside it. Shouldn’t the answer be D in this situation? How can we assume the center of the circle lies on the triangle’s side? Could you clarify my misunderstanding?
C is supposed to be the circumcenter, so it’s the blue point. In particular, it’ll be positioned halfway through your hypotenuse.
I see. So, can we conclude that whenever a right triangle is circumscribed in a circle, the center of the circle will always lie on the hypotenuse?
Additionally, could you please guide me to resources for a quick revision of these properties?
Yeah, the center of the circumscribed circle will be midway between the hypotenuse. That’s because the circumradius (distance from this center to one of the vertices) is just half the hypotenuse, as you may have noticed.
Also remember that “center of triangle” can be any type of centers, so yeah we’re strictly talking about the circumcenter here.
That makes sense. Thanks very much
Additionally, if you have any recommendations for this, I would be grateful.
Idk