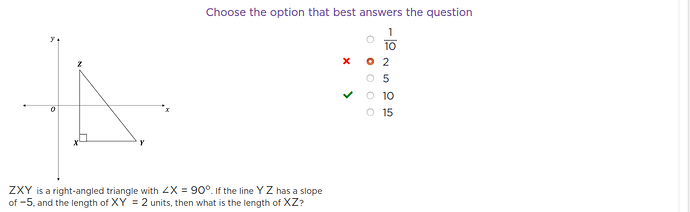
tan(angle XYZ) = XZ/XY
given slope of line ZY = -5 which is equal to -1 * tan(angle XYZ)
Therefore tan(angle XYZ) = 5
5= XZ/2
XZ = 10
Can u solve it another way ?
If you use equation of slope \frac{y_2-y_1}{x_2-x_1} and right triangle equation H^2=P^2+B^2, you’ll get an answer in the lines of 10.xxx
I’m going to name angles as <X, <Y, <Z corresponding to the vertices. For line YZ, you know the slope is -5. Also this slope equal to -tan(<Y) ( trigo property : tan(180* - <Y) = -tan(<Y) ). Also we know tan(<Y) = ZX/XY i.e. -(slope of ZY) = ZX/XY . Solving this equation gives ZX = 5. Btw, you don’t need that trigo property, as when you solve with tan(<Y) = -5, you’ll get ZX = 5. Since length can’t be negative, it must be 5 then.
@HoldMyBeer it worked for me, thank you 
Got exactly 10 after aligning the triangle to 1st quadrant.
This is much quicker and easier. Thanks.