Counting problem: How many times the word **DIRECTOR** can be rearrange

GRE Quant Problem Solving
1

How many times the word DIRECTOR can be rearrange without changing the order of vowels?

2

There are 2 ways of solving this problem.

  1. The problem says we shouldn’t change the order of the vowels, the vowels in the question are I-E-O and we have to maintain the same order. So, 3 characters cannot be rearranged. The rest can still be rearranged. So Let’s consider 8 empty boxes where we need to fill the 8 characters we have.
    image
    We have the consonants D-R-C-T-R. Let us first arrange that. The number of ways to do that is first you choose 5 spaces out of 8 (which can be done in 8C5 ways), and fill those 5 spaces with the consonants ( filling 5 boxes with 5 consonants where two of them are similar - 2 Rs - 5P5 / 2! ).
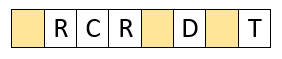
    image
    The above might be one of the possibilities of what we just calculated so far. 5 boxes were selected and filled with consonants. Now, of the 3 boxes, we don’t have a choice to arrange the vowels. So the order will be I-E-O which is only 1 possible way. So, your final answer will be (8C5 x 5P5) / (2!)

  2. Second way is to assume that all your vowels are the same (meaning that there is only one way of arranging them). So your word has 8 characters and 2 of them are of the same kind (Rs) and 3 of them are of the same kind (vowels) as well. So your final answer will be (8P8) / (2! * 3!)