Hi,
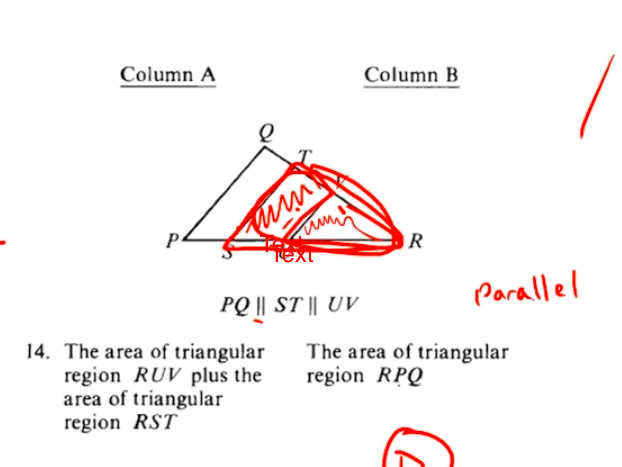
Isn’t Quantity A here only a part of Quantity B? Can someone explain why the answer isn’t B?
Also, is there more information on finding the height and base in similar triangles?
The area of triangle RST includes the area of triangle RUV. The sum of RUV plus RST is 2x the area of RUV, plus the remaining quadrilateral area UVTS.
Scenario 1: imagine RU is almost as long as RS, and RS almost as long as RP. In this case, area of RUV plus area of RST is nearly double the area of RPQ.
Scenario 2: imagine RU is almost as long as RS, but now, RS is 1% of the length of RP. In this case, area of RUV + area of RST is much, much smaller than the area of RPQ.
Answer = D
Can you share an image of the solution. I am not sure I understand.
Plus, if you can suggest a source for this knowledge.
Visual aid:
Case 1: RST + RUV > RPQ
Case 2: RST + RUV < RPQ
Slide 101 of the math review guide has GRE-specific similar triangles content: https://www.ets.org/pdfs/gre/gre-math-review.pdf
Helps a lot. Thank you.
1 Like