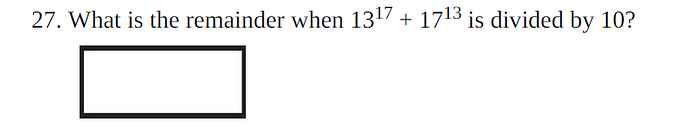I was practicing on this question, it is not coming from your material or ets official material, however i want to ask you if i can solve the problem in this way:
since a know that Phi(17) is 16 because 17 is a prime number as well as Phi(13) is 12, i can go on simplifying the exponent in this way:
16 mod 10 = 6
12 mod 10 = 2
then i can do it also for the base
13 mod 10 = 3
17 mod 10 = 7
Now i have the expression in this form 3^6 + 7^2 that can be easily simplified to:
729 + 289 = 1018 mod 10 equals 8
So the remainder is 8
Probably you don’t know what Euler’s totient function is, i am of BS CS student in Italy so this approach could be quite difficult.
Hope you can help me
Regards
Uhh what, that’s not how euler’s/ fermat’s little theorem works.
You want something like this:
13 \equiv 3 \pmod{10} and 17 \equiv 7 \pmod{10}
and so 13^{17} \pmod{10} = 3^{17} \pmod{10}
you know that \phi(17) = 16 thus 3^{16} \equiv 1 \pmod{10} and so 3^{17} \equiv 3 \pmod{10}.
In a similar fashion, 17^{13} \pmod{10} = 7^{13} \pmod{10} = 7^{12} \cdot 7 \pmod{10} = 7 \pmod{10}
and so (13^{17} + 17^{13}) \pmod{10} = (7 + 3) \pmod{10} = 0
No need for such condescension lol.