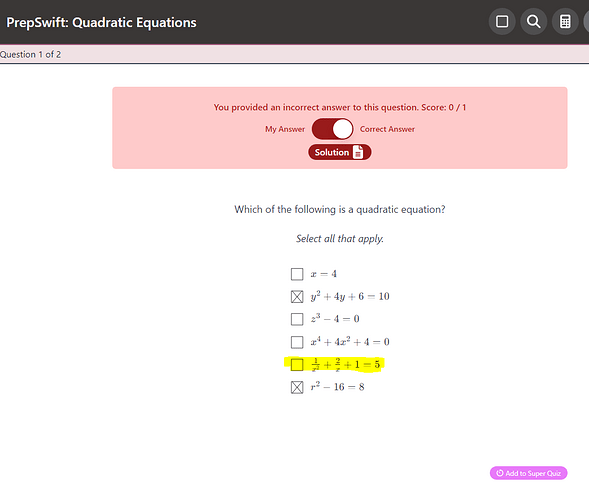
Why we are not considering the yellow highlighted one as Quadratic Equation? Solution says it has negative power, but can’t we multiply it by x^2?
What’s the degree of a quadratic equation?
And what’s the degree of the highlighted equation?
2
. 0.5
But, we can multiply the equation by x^2 and it will become a quadratic equation.
Let’s just say that multiplying by x^2 makes it a quadratic equation. That basically means it is currently NOT a quadratic equation. Isn’t that what the question is asking?
Also, 0.5 is not the degree. The first term has a degree of -2, 2nd term has a degree of -1 and the 3rd term has a degree of zero. Highest degree = 0 = degree of the polynomial.
Degree of quadratic polynomial = 2.
still not convinsed for the 1st part. currently NOT a quadratic equation but it is equivalent for a quadratic equation (except for x=0) ?? ![]()
and, my bad for 2nd part. ![]()
By multiplying by x^2, you are increasing the degree of each term by 2.
4x^2 - 2x - 1 =0 is indeed a quadratic equation. These 2 when plotted will have the same graph, however in the form as highlighted, it is not a quadratic equation.