If the height of the inscribed equilateral triangle is 6, what is the area of the circle?
A. 9π
B. 12π
C. 16π
D. 24π
E. 36π
1 Like
The key concept is that, in an equilateral triangle inscribed in a circle, the ratio of the intersection of medians is 2:1 from vertex to intersection point vs till the rest of opposite side, and here the height = median.
So, height = 6, then the intersection length would be 4, now this is the center of the circle since the triangle had been inscribed in the circle. So, radius = 4.
area = πr^2 = π16 = 16π
C. 16π
2 Likes
First find the side of triangle : 30-60-90 property --> you will find side (S) = 12/root3
Now just remember this relationship if the circle is touched by all the three vertex of an equilateral triangle then side = radius x root 3
we know the side so radius = 4
Area = pi x r^2 = 16pi
1 Like
Todayβs problem of the days and daily exercises are just released! Check your answer here: https://new.gregmat.com/daily
hey! thanks for the explanation. Does Greg talk about this βkey conceptβ in his geo concept lessons? i havenβt gone through them yet
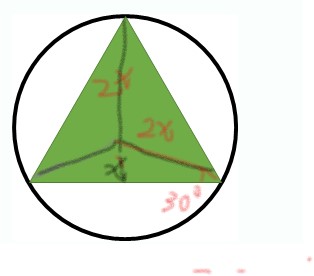
As it is drawn above, 2x+x=3x constitutes the height of the triangle. Thus, x=2,2x=4 which is the radius of the circle.
no need to do such complicated calculation, Mr.Putin Lol
Is this true for any equilateral triangle or just for an equilateral triangle inscribed in a circle?
It is true to any equilateral triangle. This property is derived from trigonometry theorem.
1 Like
The property of intersection of the medians of a triangle. The centroid of a triangle | MATHVOX
It is true for any equilateral triangle.
1 Like
This is quite a goos solution. 30-60-90 solutions are more intuitive, and help us arrive at the answer without knowing a key theorem about equilateral triangle centroids.
1 Like