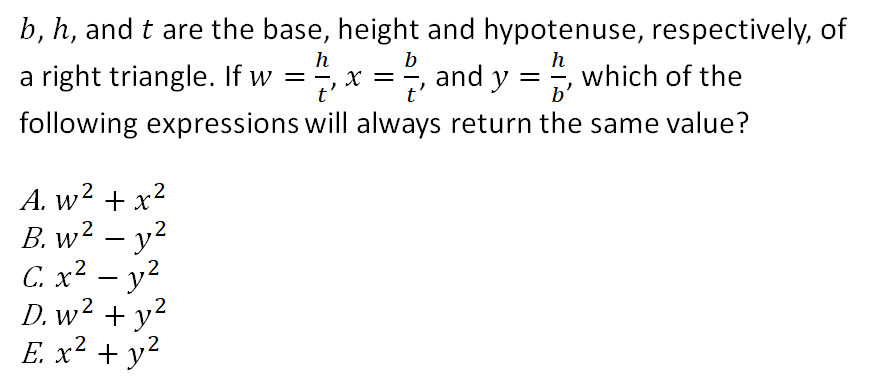I didn’t quite understand what exactly was the question asking us to find but here is what I thought it did :
From the question we get : t^2 = h^2 + b^2 —(Pythagoras Theorem )
from this option A will always be 1. So for all the values of w^2 and x^2 this expression will remain the same
One more way to look at it, using trigonometry identities
Assuming angle a between b and t.
cos(a)=h/t
sin(a)=b/t
tan(a)=h/b
Hence correct answer is A
cos^2(a)+sin^2(a)=1 ; For any values of b,t,h
basically, this question can be sloved by that cos 
^2+sin ^2=1, where cos =x,sin =w
the value of A is always 1
t^2 = h^2+b^2
Therefore, 1= (h^2+b^2)/t^2
A. w^2 + x^2 = (h^2+b^2)/t^2 = 1
this equation shows “(h^2+b^2)/t^2 = 1”, whatever the value of t,h,b is- the answer will always be 1
Therefore, A is correct
I’m thinking of ( t^2=h^2+b^2) could t^2 be divided by the whole equation ? isn’t it
H^2+b^2-t^2=0 if we want to take it to the other side ?
Or we can do both ?
Its better to divide t^2 on both sides because then we directly get option a. We can do the other thing too but that wont return us any result