EXTREME Quant Problem of the Day May 3rd, 2021

GRE Quant Problem Solving
1

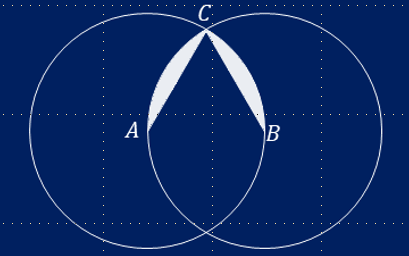
image

image
image1068×257 5.49 KB

5

I think its A. Where can i find the solution to check?

6
8

image
Find area of the shared portion between 2 circle - 2(Area of Equilateral triangle)= Area of the borders. Half of that will be the answer(for our ease take pi= 3 and root 3 = 2)

1 Like
9
  1. We have radius = 6 and we have equilateral triangle with side = 6
  2. We find the area of the triangle = 9√3 or 15.58
  3. We find the area of the circle which is going to be 36π.
  4. We find the area of the segment which is 1/6 of the total area of the circle. We get 6π.
  5. We substract are of the triangle from the area of segment. 6π - 9√3 = 18.84 - 15.58 = 3.26
  6. As we have two such shaded regions 3.26 * 2 = 6.52
10

Yes

11

Can you always find the square root result of a number and keep it precisely to 2 decimals?

I’m not sure how did you get this number without using a calculator? 1.7*9=15.3,wherase 1.8*9 =16.2, the only way you had this 15.58 is you took \sqrt{3} as 1.73, but the problem is how did you know so precisely? What would u say the approximate decimal of \sqrt{7} , \sqrt{5} ? like how to manually get it into two decimals form？

12

9√3 is the same as √ 81 * √3 which is √243. Taking the square root of √243, you will have 15.58

13

Appreciate your reply but you are not answering my question. My question is, how do you manage to break down a root number into its 2 decimals form manually? Anything special with \sqrt{243} ? Don’t we still need to bring in our calculator?

14

Sorry. I guess there is nothing special with taking approximate square root of any number. I would suggest you learn by heart “Square numbers” up to 40. The strategy that I use is for example in the case with √243. I know that √243 is between √225 (which is 15) and √256 (which is 16). But it lies a bit close to √256 and my guess would be something around 15.6 or 15.7.

1 Like
15

The calculator on the GRE does have a square root function

16

@gregmat Are Extreme Quant problems of the day meant to be similar in difficulty to the “Hard” (as opposed to Easy or Medium) second section of GRE Quant?

17

In some cases yes, but I think they’re sometimes even harder than what you’ll see