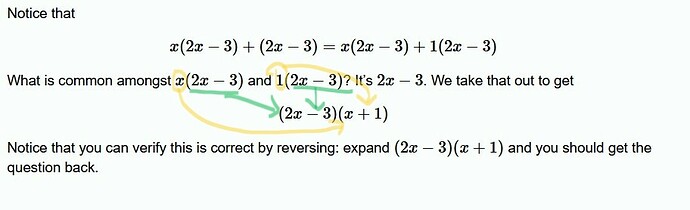Hi guys, can anyone help me out here. I’m watching a video on factoring quadratic equations that are not easy to factor. Please see the image for a stepwise approach. I just don’t understand the final step. For the final step Greg says: “we have 2x-3 in common so we can pull that out”, but I really don’t understand how that results in the last step. Thanks for your help.
Hint: you can write (2x - 3) as 1(2x - 3). Then the circled step can be written as
x(2x - 3) + 1(2x - 3)
Can you now complete the last step?
Thanks @Leaderboard, yes, I was guessing something like this but I’m not sure if I really understand the theory/math behind it. Sorry, started from scratch with the math.
So I understand we have an x and a 1 remaining and we cannot ignore, so they form the (x+1). But to me it now looks like one of the 2x-3 is disappearing. Yes, they are common so we are pulling them out but pulling out from what. Sorry if my question is weird.
I did validate (2x-3)(x+1) by foiling and the original equation is the result, so I do see that it all makes sense but the pulling out just remains a bit blurry to me.
Try multiplying the result of the last step.
I’m having trouble understanding the explanation on the video as well.
He states (2x-3) is the common term that can be pulled out of both terms then wouldn’t you end up with just x+1 by itself?
How is one of the (2x-3) terms still brought down to the next step?
What do you mean?
If he states you “pull out” (2x-3) from both terms, wouldn’t the (2x-3) disappear then? Leaving you with only (x+1)?
How are you getting from this step to the step below. It’s not clear in the video or earlier explanations on how you are “pulling (2x-3) from both terms” to get to (2x-3) (x+1) on the last line.
Notice that
What is common amongst x(2x - 3) and 1(2x - 3)? It’s 2x - 3. We take that out to get
Notice that you can verify this is correct by reversing: expand (2x - 3)(x + 1) and you should get the question back.
Ok, so based on the other examples on the video too, you’re pulling out the (2x-3) and then whatever is in front of the two parentheses you are making that another term in parenthesis? Is there a name for this technique or what you’re doing here? I don’t think I see this particular technique in a previous video.
It’s called factoring by grouping. See Factoring by grouping (article) | Khan Academy
Thank you for the quick responses and clarification. Appreciate the link.