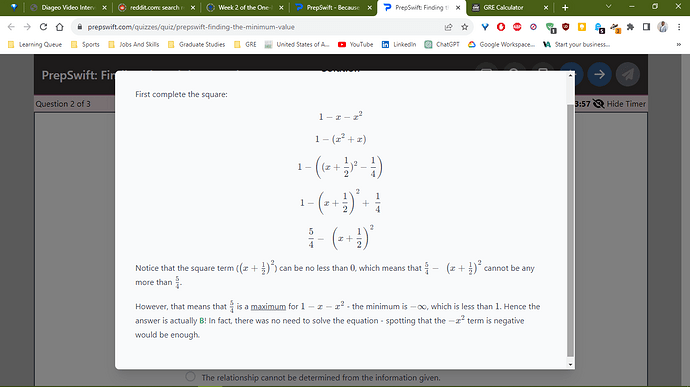
Is this saying that the minimum value is less than one whenever the x^2 term is negative? I seem to remember that some of Greg’s questions prior to this gave us upward-facing parabolas that were in the 1st and 3rd quadrants.
The minimum value is -\infty if the x^2 term is negative.
Ok. I now see why I got this question wrong. I don’t remember Greg ever mentioning that when the parabola points upward, the vertex is the “maximum value”. This means that a quadratic with a positive x^2 term will have a maximum value of + infinity right?
Correct.
1 Like