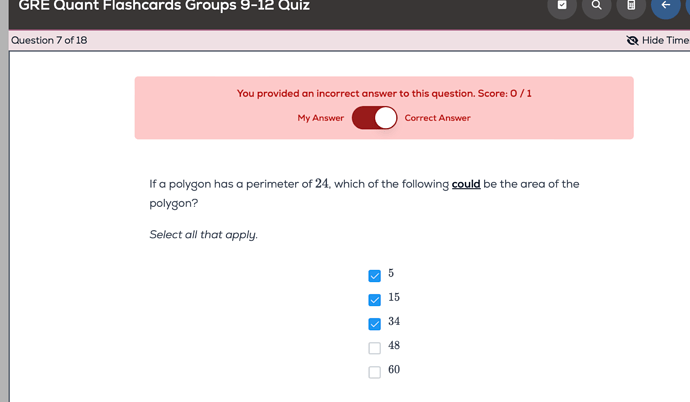
For the following question (from Greg Mat’s Flashcards Quiz for Groups 9-12), I followed the procedure outlined in Group 10’s “Quant Flashcards” under “Regular Polygon Area”. Following the steps outlined on the flashcard, I took the polygon’s perimeter and multiplied it by the triangle’s height and divided this by 2.
When I followed this procedure with a hexagon (each side has a length of 4), I got 24√3 (which is approximately 41.6). When I followed this procedure with a triangle (each side has a length of 8), I got 48√3, which is approximately 83.
I have not been able to find a way to get any answer below 41. Also, I couldn’t find an explanation that accompanies (in text or video) the correct answers. If they are on the website, can someone please point them out.
Ultimately, can someone please explain how to approach this question to get answers 5, 15, and 34.
Hint: the area can be very close to 0. Try an example.
1 Like
Thanks for the reply.
I further worked on this question and found that a 48-sided polygon, with perimeter 24, can produce a 5.1 area. I imagine that if I were to increase the number of sides to 72 sides or some other multiple of 24 that I can get close to 0.
However, how is the maximum 34? (I think that this is an extreme/boundary question.) Polygons that are 6 or 8 sides, with perimeter 24, can yield an area of 83.
Does Greg Mat provide explanations for correct answers for Flashcards quizzes (especially for groups 9 to 12)? If so, can someone please direct me to them.
Hey,
I think in every case you are trying to calculate the are of the polygon by considering a regular polygon. But what we have here is a Polygon which can have varying side lengths. So by considering the extreme polygon(which is a circle with infinite sides), the area of the circle with 24 as its perimeter we get 45.9 which is our extreme here. Hence we are choosing all the values less than 45.9 as the question says “COULD BE”
This is just my hunch, @Leaderboard correct me if I’m wrong.
2 Likes
Thank you so much for the explanation, @rsruthi48
To clarify, a circle (although not itself a polygon) would provide the upper bound (extreme) for the area of a 24-perimeter polygon. Zero would act as the lower bound (extreme). Neither zero nor a circle’s area could be the answer, but any answers in-between these two could be the answers. Is this right?
Although the question doesn’t state that it has to be a regular polygon, it could be a regular polygon, right? I am still somewhat confused as to why the extreme bound of the area cannot be higher (had it been a regular polygon).
To clarify, a circle (although not itself a polygon) would provide the upper bound (extreme) for the area of a 24-perimeter polygon. Zero would act as the lower bound (extreme). Neither zero nor a circle’s area could be the answer, but any answers in-between these two could be the answers. Is this right?
“Yes right”
Although the question doesn’t state that it has to be a regular polygon, it could be a regular polygon, right? I am still somewhat confused as to why the extreme bound of the area cannot be higher (had it been a regular polygon).
“Yes it doesnt state its a regular polygon so our hunch is to consider a Polygon with varying side lengths. Lets assume its a regular polygon, 3,4,5,6,… will be our varying sides upto infinity which is a circle ultimately, so having 3 sides the area would be 27, for 4 sides its 36 and it goes on. With a regular Polygon the area is definite for any number of sides, but for a Polygon as the side lengths vary the height of the triangle varies and the area is not fixed. So its best to consider a Polygon instead of a Regular Polygon”
Hope this helps, This is just my hunch @Leaderboard correct me if I’m wrong.
1 Like
Thank you so much for taking the time to help with this math question –– I so appreciate it!
I would think that we should consider both possibilities (regular and irregular) to get both extremes (especially the maximum), but I gather that because the question doesn’t use the word “regular” polygons, we should only consider irregular polygons. Is this right, according to your understanding?