Flashcards Quiz 9-12 + another question

[user1454]

Hi,

1. I first divided the total number of students by 100 to determine how many students are in each percentile. Since 170 is the highest score and the 96th percentile is mentioned, I assumed it covers the range from the 96th to the 99th percentile. I multiplied the number of students per percentile by 3 or 4 to estimate, and the closest result was 55,000. Is my approach correct?
   

   

2. Why did Greg say the word “regular” caused a problem here? What would the correct approach have been? If the word “regular” wasn’t included, the minimum wouldn’t necessarily be an equilateral triangle. So, how would we calculate the minimum in that case?
   

   

3. Why was it necessary to include the word “max”? What interpretation could have been made without “max” that would have made option D correct (Greg mentioned it)?
   

   

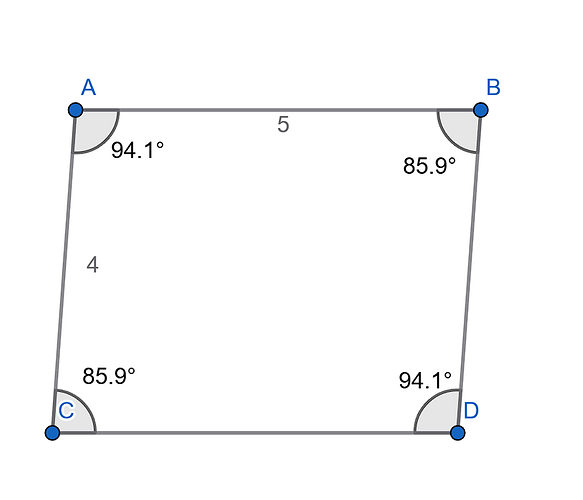
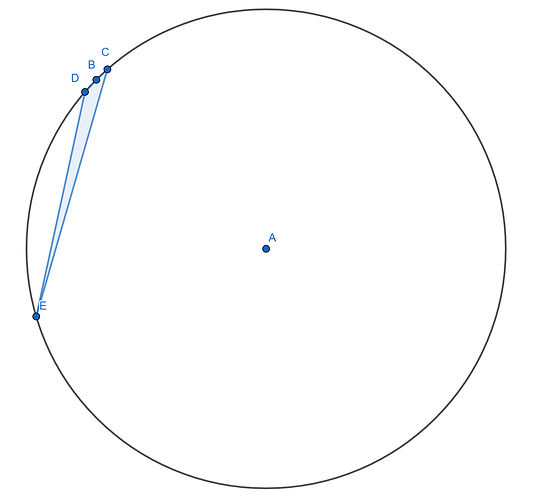
4. How can a quadrilateral inscribed in a circle with a radius of 15 have an area less than 1? No matter how I calculate it, considering the circle’s radius of 15, the quadrilateral’s area should definitely be greater than 1.
   

   

[cylverixxx]

1. Yes

2. The minimum would just be 0 in the case of an irregular polygon. The maximum, however, is fixed regardless of whether the polygon is regular or not.

Quantity A without “max”:

Quantity B without “max”:

You can consider a rectangle with dimensions (8,1,8,1), whose area then is 8.

[user1454]

Hello,

Thank you so much for your clear explanation.

Could you please just explain the question 2 (based on the inclusion of the word “regular”) and the question 3 (based on the inclusion of the word “max area”) ?

[cylverixxx]

@user1454

question 3 (based on the inclusion of the word “max area”) ?

It’s shown in the image I made for you above, where we illustrated that there are configurations in which the area of a parallelogram is greater than that of a rectangle with the same perimeter. Without the word “max”, the answer would consequently be D for the aforementioned reasons.

@user1454

Could you please just explain the question 2 (based on the inclusion of the word “regular”)

Not sure what else to add besides what was previously mentioned.

To reiterate, among regular polygons with a fixed perimeter, the smallest area is that of the equilateral triangle. In contrast, if you allow irregular polygons— you can imagine the exact scenario in my image I provided for question 4—the minimum area would approach zero. That’s the only difference when removing the word “regular” from the question.