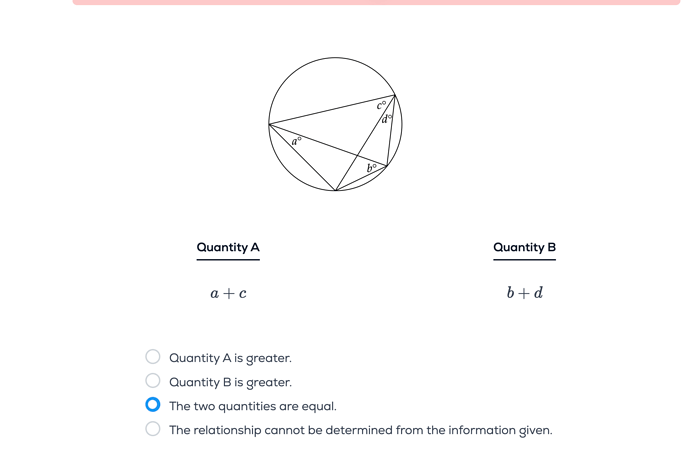
According to the video a and d are equal due to both their legs hitting the circle at the same point, I am not sure why this would mean the angles would be necessarily equal. As the circle doesn’t necessarily need to be drawn to scale and one can observe the point next to d could even be drawn on the top edge of the circle, would a still = d in that situation
points where the angle a and d is measured are on the circle. And their legs touch the same arc of the circle. By inscribed angle theorem (not sure if in video), both the angles are the same, since they intercept the same arc.
It’s necessary that the point should be on the circle. And I believe that will usually be the case unless mentioned, or drawn
1 Like
Thanks I found a good video on the inscribed angle theorem from Khan Academy, pretty insightful