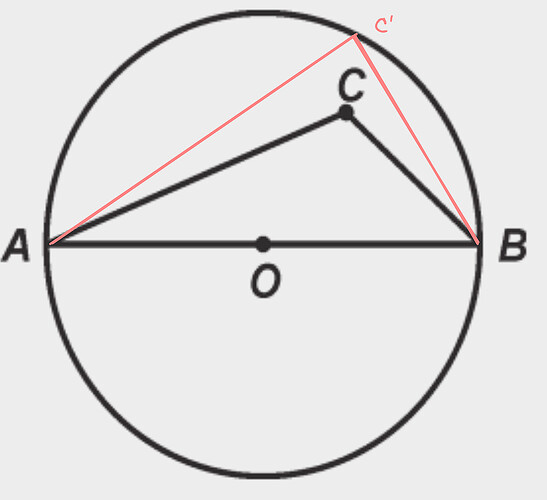
Greg has explained this somewhere but I am unable to find his explanation. At the circumference this angle is 90 so shouldn’t it be less inside the circle. Answer key shows that Quantity A is greater. How? On a related note, my question is also about the measure of the angle outside the circle by the same diameter AB. Would be grateful if you could explain this/
If you pull the point C down into the circle, AB stays the same, but AC and BC reduces right?
What happens to the ratio of the size of AB to the other sides, does it go up or go down?
And as a result, should the angle opposite AB (angle at C) go up or go down?
By that logic, placing C near A (on the circumference) and then translating in space to C’ (where C is now) would suggest that AC has increased while BC has decreased. Not sure if i’m missing something from your argument, but as it stands you can’t say much about \angle ACB, no?
But in this case, position of point C is fixed right so how does this case apply here?
Why do you say it’s fixed?
I could be wrong but based on ETS assumptions and guidelines for geometry figures the positions of given points are fixed but again its such a grey area to me so its good to confirm these assumptions
C can’t be on the circumference, but it’s anywhere “above” AB
yeah that makes more sense.
Anyway, do you have any ideas as to how to “solve” this question? The very first idea I had was to extend line segment BC and AC such that it intersects with the circumference of the circle. If you wish, then we can proceed with this idea unless you want to implement whatever you had in mind instead.
Yes, let’s proceed. I think Ganesh’s explanation makes sense, as side AC pulls the angle toward it, reducing the length of the other sides. Your point about C being near the circumference is interesting, but I believe angle ACB would still be greater than 90 degrees, since AB is the longest side, being the diameter of the circle. Thus, the lengths of AC and BC will always be less than AC. The only scenario where any side can be greater than the diameter is if point C is outside the circle. Otherwise, if C is inside, angle ACB will be greater than 90 degrees. I am drawing this parallel from Pythagoras because when the angle is 90 degrees, the sum of the squares of the sides equals the hypotenuse. However, if the hypotenuse is kept fixed and we begin to bring an angle closer to it, the angle opposite the hypotenuse continues to increase. Here hypotenuse being the diameter of the circle. Not sure if this is a correct analogy to bring here.
What do you think?
I think ganesh’s argument was something like the above. If you pull C’ down to C then C must be greater than 90^{\circ} to “produce” the same AB because of AC' and AB' being shrinked. Nothing wrong with this here.
However, this pictorial argument just captures a very narrow case and doesn’t really answer the question generally. For example, consider the below image.
Now AC' gets enlarged and BC' gets shrinked when transitioning from \triangle AC'B to \triangle ACB. As it stands, you can’t just straightaway claim how \angle AC'B compares to \angle ACB. I’m guessing your entire explanation hinged on the first image, and thus doesn’t apply to the second image and other similar cases.
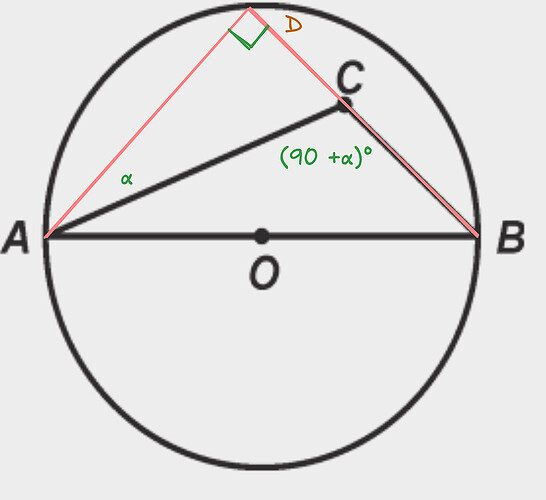
Anyway, my idea was something like this:
Assume that the minor arc DE has “angle measure” of x^{\circ}, then can you show that \angle ECD = \angle ACB = \frac{180^{\circ} + x^{\circ}}{2} = \left(90 + \frac x2\right)^{\circ}? Since we know that x > 0 (unless we consider the degenerate case of D being coincident with E; this case is not interesting because you already know what happens here), then \left(90 + \frac x2\right)^{\circ} > 90^{\circ} implying \angle ACB > 90
That’s very smart. Yes, I understood the proof you did. Correct me if I am wrong, Since arc DE measures x and C is the angle inside the circle. The arc opposite to angle C in addition to DE is arc AB (the semi circle and the measure of arc AB is 180 so going by the property - angle C = (arc measure DE + arc measure AB)/ 2. In this case, angle C = (x+180)/2 thereby proving that angle C is 90 + x/2. Thank you so much. This is so helpful.
In case anyone is interested in understanding this concept a bit more through more examples and visualization. You can watch this amazing explanation about other such properties by Danny Chang - https://www.youtube.com/watch?v=yuG6joJk3oQ
This video for sure helped me in understanding cylverixxx’s explanation better ![]()
Yeah, that sounds like it.
Btw here’s a more approachable (not necessarily easier) “method” for gre purposes
hmmm exterior angle property. This is also good to know . Amazing stuff, cylverixxx. Thanks for your help and time. Also, thank you, Ganesh for sharing your insights. They offered a different and interesting POV and were super helpful.