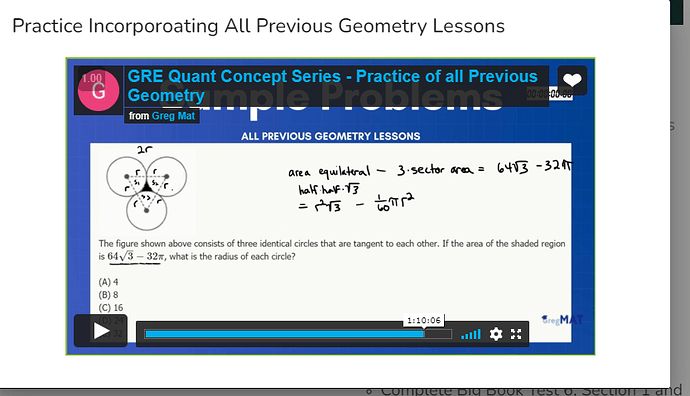
Where did the 1/60 came from in the 1/60 pie r square?
It should be \frac{1}{6}\pi r^2, not 60.
Notice that the triangle is equilateral, so the all angles are 60. Also, notice that when we substract the shaded area, we have three identical sector areas of circles with an angle of 60. Thus, we know that each area is \frac{60}{360}=\frac{x}{\pi r^2}, so each area is x=\frac{1}{6}\pi r^2, so the left side of his equation should be r^2\sqrt{3}-3\frac{1}{6}\pi r^2