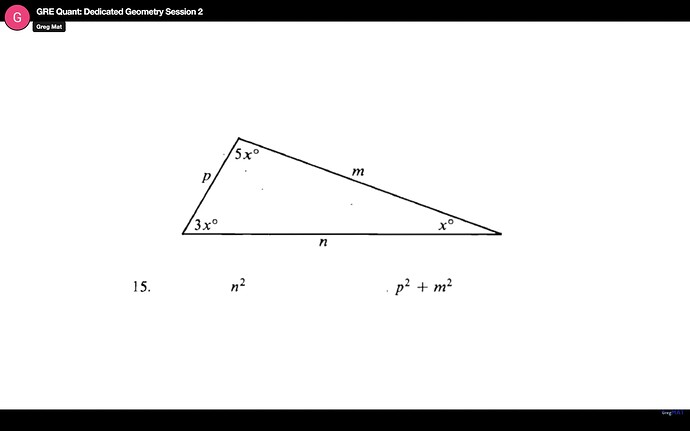
Can someone help me understand why my logic is wrong? I tried to apply the triangle rules by understanding that n > m > p. So I thought that p2 + m2 would have to be greater than n2, since the sum of 2 sides of a triangle must be greater than the one side. Why does that not work here?
Triangle inequality isn’t at play here, but rather the converse of pythagorean:
-
n^2 = m^2 + p^2 implies it’s a right angled triangle
-
n^2 > m^2 + p^2 implies it’s an obtuse triangle
-
n^2 < m^2 + p^2 implies it’s an acute triangle
The triangle inequality just says
|m - p| < n < m + p and not anything about n^2 itself