I also seem to have difficulty with QC Geometry questions, so if anyone can provide some useful tips that would be helpful. I seem to not understand a lot of the ones where D ends up being the answer.
Thanks!
As Greg always says, try to use the “equal and not equal” strategy, and do not scale the given figures when not specified to do so, in QC Questions
for example, in the 2nd last question, for the area of the rectangle, we need the length and as well as the width of the same, but only the data of length has been provided, which is 7, but we don’t know anything about the width.
let width = 4, now, AD=CB=4, and let ED = 10 and CF= 5 [since, EF=22, and DC=AB=7]
So, the Area of the Rectangle = 7x4=28 sq. units.
Area of triangle ADE = [(10x4)/2] = 20 sq.units.
In this case, the Answer is A.
But, let width = 4, now, AD=CB=4, and let ED = 14 and CF= 1 [since, EF=22, and DC=AB=7]
So, the Area of the Rectangle = 7x4=28 sq. units.
Area of triangle ADE = [(14x4)/2] = 28 sq.units.
In this case, the Answer is C.
Therefore, In one case we received A and in the other case we received C, So the actual Answer is D.
In 1st question, CT=30 inches= radius of the larger circle, and
CN=8 inches= radius of the smaller circle.
Therefore, the Area of the Shaded Region = [(The Area of the larger circle) - (The Area of the smaller Circle)]
the Area of the Shaded Region = [πx(30)^2] - [πx(8)^2]
the Area of the Shaded Region = [900π - 64π] = 836 π
Therefore, the Answer is A.
For the 2nd question,
You need to know about 1 concept related to the exterior angles theorem, which states that, exterior angle = the summation of two opposite interior angles.
Therefore, for angle x, opposite angle interior angles are 20 and 50, so,
angle x = 20 + 50 = 70 degrees, again, similarly,
angle y = 80 + 50 = 130 degrees. (why 80?, it is because 60 + 20)
so, x + y= 130 +70 = 200.
The Answer is A.
For the last problem,
Always remember if, in any geometric figure, you notice the small square-like structures drawn within an angle region, actually it denotes that particular angle as 90 degrees.
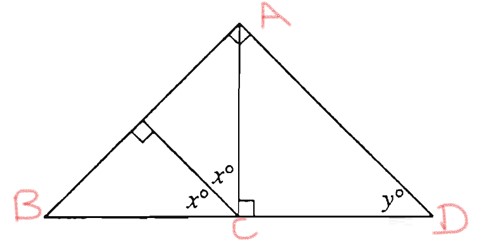
Here, angle C = 180 degrees(since the angle of a straight line = 180 degrees) again angle C = 2x + 90.
Therefore, 2x+90 = 180 => x = 45 degrees
Again, In triangle ACD, Angle ACD = 90 degrees and Angle CAD = 45 degrees(since, 90/2 = 45 degrees).
We know that sum of 3 angles of a triangle = 180 degrees.
Therefore, 90 + 45 + y = 180 => y = 45 degrees.
So, the answer is C.
Hopefully, you will get to understand this now.
Thank you for this, it was really helpful. In terms of the first one with the rectangle and two triangles, did you just choose numbers for the lengths of the triangle bases that could add up to 22?
1 Like
Yes @lindseyrosen05, you are correct
I choose numbers for the lengths of the triangle bases that could add up to 22