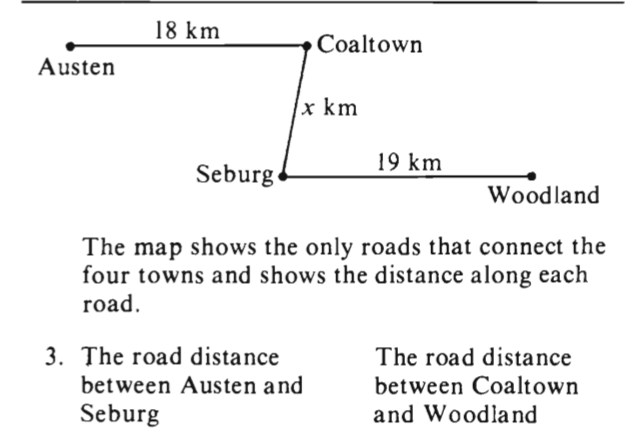
A little confused about the process for solving this problem, I thought it was D because the values can range from (19 - x) to (19 + x) and (18 - x) to (18 + x) for the two distances. I thought there would some shared values for the distance and some values that would not be shared for the distances between the towns. Thank you!
Anwser is B?
I think you dismissed the part where it says “only roads”.
You’re looking at a completely new road, which doesn’t exist in the diagram
Well I think it’s B because distance can’t be -ve.
Even if for some reason x were allowed to be negative, the answer would still not be D.
We are comparing 18 + x and 19 + x; it should be evident that 19 + x is always greater for all real values of x.
What is x ?
x is distance from coaltown to seburg.
although distance can never be -ve, as you said let’s say x is -ve integer.
Let x = -3
Now put the value of x inside the equation
19+x
19+(-3)
19-3
So this is clearly wrong.
So we can’t assume x -ve in any scenario because distance is either 0 or greater than 0.
Your whole premise is that the answer is B because x can’t be negative. However, even in the off chance that x were allowed to be negative, the comparison between 19 + x and 18 + x still yields B as the answer.
The main reason B is correct is that 19 + x > 18 + x under the stipulation that x > 0 for the situation to make physical sense. Nevertheless, even if we disregard the “physical sense” part, 19 + x > 18 + x holds for any real x.
Thus, I would argue that while “distance can’t be negative” is a true statement, it doesn’t really assert why the correct answer is what it is.