Hi,
I am stuck at the following question. I am unable to find the linkage between the area of the smaller triangle and the large triangle. How can I go about this?
Consider a 3-4-5 right triangle. What would be its area? It would be (3)(4)/2 = 6 right? Now let’s rescale the triangle to have a 6-8-10 right triangle. We know that we would these two trianlges would be similar, since the only thing that changes is the side lengths. Indeed, 6=3\cdot 2, 8=4\cdot 2, and 10=5\cdot 2. Now consider a 9-12-15 right triangle and similarly we will notice that these triangle with the 3-4-5 is similar since 9=3\cdot 3, 12=4\cdot 3, and 15=5\cdot 3.
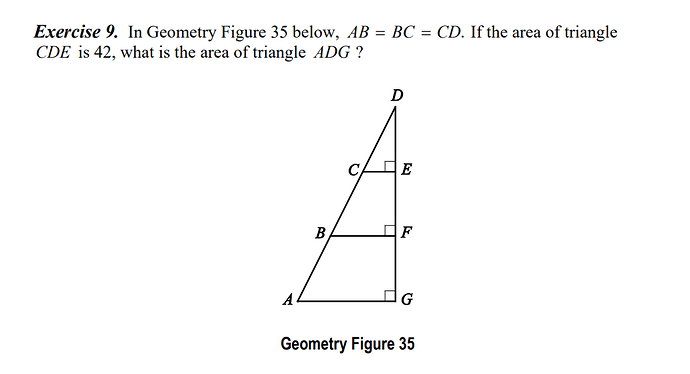
Now consider the problem at hand. Notice that triangles ADG, BDF, and CDE are similar, and given that AB=BC=CD, we have proportional sides, meaning that for triangle BDF, side BD=2CD and BF=2CE and FD=2ED. Similarly, AD=3CD and AG=3CE and GD=3ED. Since the area of CED=42, then you know that (CE)(ED)/2=42. Now, the area of AGD is (AG)(GD)/2 = (3CE)(3ED)/2 = (3)(3)(CE)(ED)/2 =9*42=378.
The key is noticing that the triangles CED, BFD and AGD have the exact same angles, so their sides are proportionals. Hope this sheds some light!