GRE Quant Foundation Assessment Test (Data Analysis - Part 2) {Mutually Exclusive maximum value}

GRE Quant Problem Solving
1

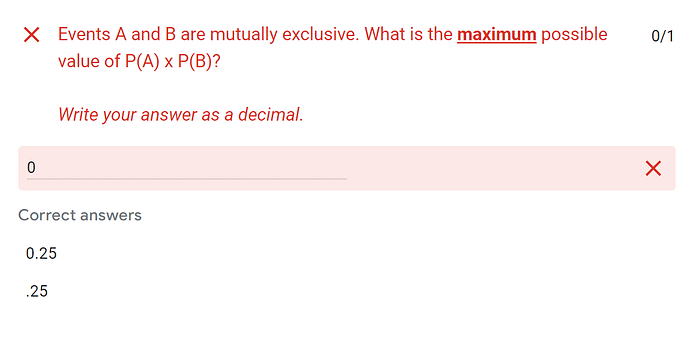
This problem is really interesting because while attempting it I wrote the answer as 0 as these are mutually exclusive events so they can’t happen at the same time which is to say I assumed that P(A)*P(B) is the formula to find probability of events happening at the same time for independent even so this would definitely be 0 but I was humbled pretty quickly.

image
image1150×563 25.3 KB

So, I have two questions-

  1. even if the question mentions its maximum why would it ever go above 0 because the expression P(A)*P(B) means they happen at the same time? It seems a little counter-intuitive to me
  2. In the solution video Greg says these probabilities are maximum when they are equal so I found this derivation online to support this claim. Is it the correct way to arrive at this conclusion?

This is the proof I found online-

Step-by-Step Approach:

Let x=P(A) and y=P(B) and recall the constraint:

x+y≤1

We want to maximize the product:

x*y

We can express y in terms of x using the constraint x+y≤1. So, y=1−x. Substituting this into the product gives:

xy=x(1−x)=x−x^2

Now, we have the function f(x)=x−x^2 and we want to find the maximum value of this expression.

Step 1: Complete the Square

We can rewrite the quadratic expression f(x)=x−x^2 by completing the square.

Now, to complete the square, factor out the negative sign from the quadratic term:

f(x)=−(x^2 -x)

f(x)=−(x2−x+1/4−1/4)

This simplifies to:

f(x)=−((x−1/2)^2−1/4)

Step 2: Analyze the Expression

The expression f(x)=−(x−12)^2+1/4 shows that the function f(x) is a downward-opening parabola with a maximum value of 1/4

Step 3: Conclusion

Since the maximum value of f(x)=x(1−x) occurs when x=1/2, the maximum possible value of P(A)×P(B) is 1/4

2

The learning here is that A x B is NOT the same as “the probability of both”.

The probability of BOTH is:

  1. 0 for mutually exclusive events
  2. A x B for independent events
  3. The smaller of A or B for complete dependence

This question is simply asking how we can maximize A x B, and NOT the probability of both.

You need to reframe the problem in this way:

A + B would equal 1, so we set up different combinations of A and B and see what A x B is:

A = 0.1, B = 0.9 → A x B = 0.09
A = 0.2, B = 0.8 → A x B = 0.16
…
A = 0.5, B = 0.5 → A x B = 0.25

In this case, the probability of BOTH is 0, since A and B are mutually exclusive, but A x B is 0.25.

This is similar to maximizing the area of a rectangle (A and B are length and width) with a fixed perimeter. If you make it into a square and split the perimeter equally (make A and B equal) then you will get the biggest value of A x B (area of the rectangle).

Does this make sense?

1 Like
3

This is so well explained! Thank you very much. These quiz questions are very meticulously framed!

1 Like