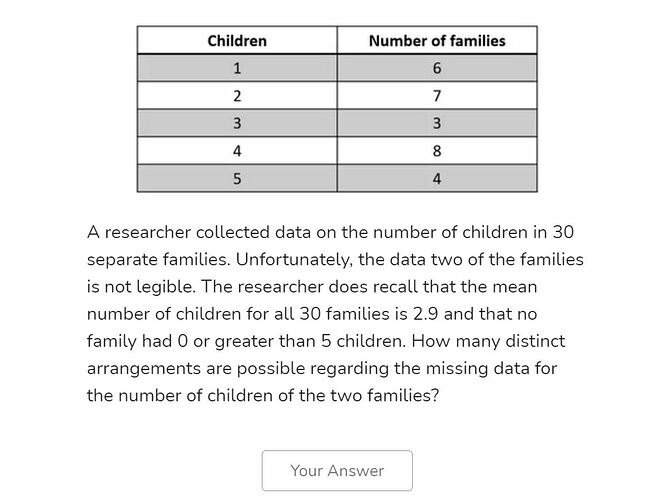
A researcher collected data on the number of children in 30 separate families. Unfortunately, the data for two of the families is not legible, but the researcher does recall that the mean number of children for all 30 families is 2.9 and that no family had 0 or greater than 5 children. How many distinct arrangements are possible regarding the missing data for the number of children of the two families?
Identical question is covered at https://youtu.be/Q3wA7Mew3TA?t=2016
Thanks, @Leaderboard!
A researcher collected data on the number of children in 30 separate families. Unfortunately, the data for two of the families is not legible, but the researcher does recall that the mean number of children for all 30 families is 2.9 and that no family had 0 or greater than 5 children. How many distinct arrangements are possible regarding the missing data for the number of children of the two families?
I think you link something else
- Find the sum
- See how much values you’re missing (hint : Original sum - sum of values in table = No. of missing values)
- calculate in how many ways you can arrange those missing values between two families
Apologies, that’s been fixed.
Number of kids in 2 illegible families = x
Mean = \frac{6+14+9+32+20+x}{30} = \frac{81+x}{30} = 2.9
81+x = 2.9 * 30 = 87
x = 6
All distinct arrangements:
Family A: 1 Family B: 5
Family A: 2 Family B: 4
Family A: 3 Family B: 3
Family A: 4 Family B: 2
Family A: 5 Family B: 1
So, ans. 5
actually 5
Yes! My bad