Hint: draw a diagram.
Is the answer 49 for this question?
Nope it’s 50 equate side of the larger square to the diagonal of smaller square so u would get 10/√2 (side of a smaller square) and area is 50
I think this Q has already been asked in this forum. @Leaderboard might link it.
Try to visualise this. But here’s the thing, let’s assume the inscribed square is literally the outer square itself. So the area would be the same as the outside square. Now move the vertex of the inscribed square say 1 unit away from the corner of the outer square, so the inner square will have it’s corners on each side of the outer square (1cm away from its corner) and the area would now decrease a bit. So the minimum would be achieved if the inscribed square’s corners are on the mid point of the outer square.
How do you know this - minimum would be achieved if the inscribed square’s corners are on the mid point of the outer square ?
Like I am hearing this for the very first time and having a hard time visualizing it.
Is this like a general fact which we have to just “learn” /mug up just the way it is?
You don’t need to mug this up. Try to visualize an outer square, and another square within overlapping the outer square. Now, Basically both the areas are the same right?

But if you move the vertices of the inner square a little away from the outer square. you leave a small triangle of area on each side.
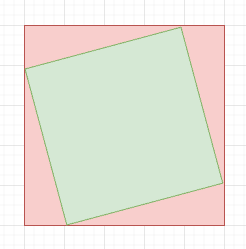
So the area would decrease.
Now you can keep doing this until you reach the middle (vertex of the inscribed square reaches the middle of the outer square). But once you pass the middle, the inscribed square will again start to become bigger and bigger.
This problem has been linked. You may also find other answers helpful in understanding