The solution is so different to what the video taught us.
I don’t understand this and I watched the video three times if I missed anything.
the whole addition thing is so new and none of the videos explain it.
What is the point of these quizzes if you are throwing such curveballs and giving us convoluted solutions.
If you multiply both quantities by AC then you’re left with:
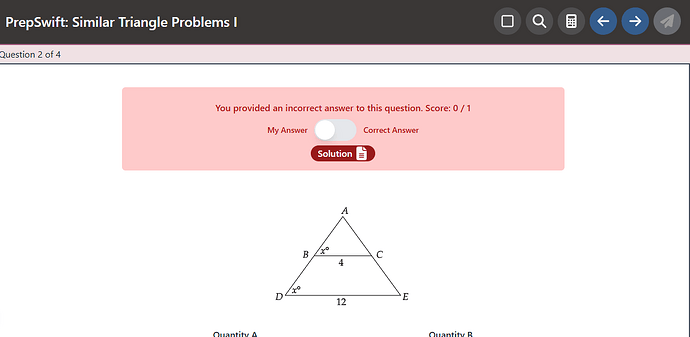
Quantity A: CE
Quantity B: 3 (AC)
From similar triangles, you know that \frac{AE}{AC} = 3 \implies AE = 3(AC) because \triangle ABC \sim \triangle ADE.
Thus, Quantity B can be rewritten to just be AE and this is clearly greater than CE thus QB > QA.
I don’t see where any “new idea” is here because it’s just elementary application of finding similar triangles and working with the information you’re presented.
your solution is even more complex to understand and doesn’t make sense either.
please break it down to simpler steps.
Do you agree that \frac{AE}{AC} = \frac 31 because triangles ABC and ADE are similar?
first where did you come to the conclusion AE/AC=3/1?
I know they are similar as mentioned in the question
Please give a step by step breakdown and this is not the only question.
There are other questions in this geometry quiz where Greg just writes stuff in solutions and tells us this is the answer.
If Prepswift is to help beginners then why are the solutions poorly written.
It gives us more questions than answers rather than telling us there is another way to write it .
Since triangles ABC and ADE are similar then you have:
\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC} = \frac{12}{4} = \frac 31
To be fair, this is just ratios of the side lengths in a similar triangle, which you should already be familiar with.
Hi OP, do you understand the solution now or do you still need a step-by-step breakdown?
Hi Greg
Can you give a step by step approach.
I apologize for being stupid for not able to solve the questions.
I am not bad with foundations as I have followed your videos and had a oh yeah moment when you solved it but this feels very complex.
Do you understand that the triangles are similar? If so, how do we know?
yes the triangles are similar
OK and do you agree that the bottom base is three times as large as the other base?
yes
So that means that AE must also be 3 times as long as AC. If we call AC x, that means AE is 3x. We can find CE by doing AE - AC = 2x