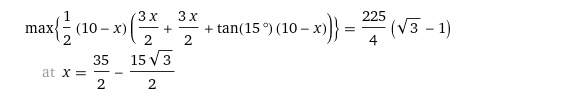Regarding the question above, The solution in the video was non-intuitive to me and I didn’t understand it.
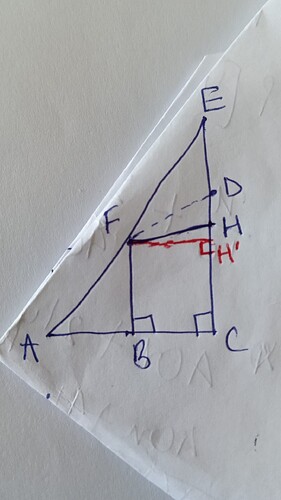
How can we be so sure that BFHC will form a rectangle? I’m also attaching a diagram to illustrate my point.
H could be closer to or same as D rather than H’. Is there a particular triangle property that I am missing here ?
Can someone please help to explain/provide a solution in a more intuitive way ?
I think you’re confusing a point here. H is not the “new D”, but rather a point such that it’s parallel to BC. Basically, BCFH is a rectangle inside the trapezoid BCDF. If the rectangle contained inside already has an area of 37.5, then it’s conceivable that the trapezoid’s area would only be more than that.
Just to clarify, the answer to Quantity A is not 37.5. It’s a bit more work to actually solve for Quantity A, which u don’t have to go through the hurdle of doing. If i were to guess, quantity A would be approximately 60-65% of the big triangle’s area.
Agreed we can make a rectangle with BCFH, I am not questioning that. But how can we conclude that if we draw a parallel line i.e. FH, then H will be the midpoint of EC ? If not, we can not assume the side length to be 7.5.
Anyways ,I was able to prove this using similarity of triangles FEH and ACE since FH || AC.
For people having similar confusion. I am sharing my version of the solution which is basically the same as Greg but more verbose.
Lets say we draw a line FH parallel to AC [as of now we do not know whether H bisects EC] but we do know that BFHC forms a rectangle. Also notice that angle BFD > 90 degrees, which means that point H will definitely fall below point D i.e. CD > CH.
Now, we need to maximize area of this rectangle. For this, we can slide B left or right [ but at the extremes , notice that it looks more and more like a rectangle]. If we have to maximize the area, it should be more regular i.e. more like a square. The closest it can come to being a square is at the midpoint. [i.e. 2BC = AC]
Now lets work on equations for similar triangles FHE and ACE.
EH/EC = FH/AC [using similarity]
[Also FH=BC since BFHC is a rectangle].
EH/EC = BC/2BC
EH/EC=1/2
so we can say that H is the midpoint of EC.
The area of rectangle now comes out to be 37.5.
Since H will always fall below D, we can certainly say that trapezoid will have an area greater than rectangle as it has an extra component of triangle FHD.
So we can say that maximum area of BCDF will be greater than 37.
1 Like
Uhhh okay.
To answer your question, I would argue:
If AC \parallel FH then \triangle FEH \sim \triangle AEC by AA. Since, \frac{EF}{EA} = \frac 12 then \frac{EH}{EC} must also be \frac 12.
This is otherwise known as the converse of the midpoint theorem.
Also, just to be clear, the configuration shown is definitely not the maximizer. Taking the area of a rectangle there is just kinda “random”. If you’ve shown that a “random” rectangle already has an area greater than 37, then it’s obvious that the maximum trapezoidal configuration would transitively have area greater than 37.
1 Like
I would like to disagree. It is definitely not random. Why ? Because random is subjective and GRE does not like subjectivity. If that’s the case, people can take B to be anywhere to conclude it is greater than, less than or equal to 37 depending on their luck. So, if my random choice of B is somewhere near the extremes, I can then conclude it will be less than 37 just because my random choice for B gives me an inaccurate insight. Of course people can try to take to all “possible” random values for B just to be sure, in which case it is no longer random.
The only way we can confidently say that it cannot not have area greater than 37 is by checking against the maximum area it can take [as stated in the question]. It makes sense too, as the more closer you are to the midpoint, the greater the area. Then after you cross midpoint, it starts decreasing again.
I am also attaching a calculus proof to illustrate that the max area will indeed occur at midpoint and it is not a co-incidence.
Maximum area of rectangle is indeed how you showed it, but well it didn’t need a whole page & calculus lol. It’s just maximizing y = \left( \frac 32 x \cdot (10-x)\right), which happens at the vertex, i.e x = 5.
HOWEVER, the x-value which maximizes the area of the rectangle is not the same as the x-value that maximizes the area of the trapezoid.
The constituents of the trapezoid is a triangle and a rectangle, and so when you maximize the area of the rectangle, you’re in turn also affecting the area of the triangle — which u don’t account for.
If you actually try to maximize the area of the trapezoid, this is what you’d be working with:
- AB = x
- BC = 10 - x
- FB = \frac 32 x
- DH = (10 - x) \tan (15^{\circ})
- DC = HC + HD = FB + DH = \frac 32x + (10 - x) \tan (15^{\circ})
Thus, when we maximize the area, we have:
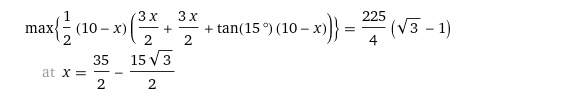
(This is obviously not when x = 5; also, this is also elementary to maximize with basic algebra — by looking at the vertex of quadratic — or calculus, and so i’m not going to bother myself into doing it)
Because random is subjective and GRE does not like subjectivity.
If the rectangle (the one chosen by greg and you) is not part of the maximized trapezoid (which is clear above) then clearly it is “random”, but that’s a fair way to solve the problem. There’s no subjectivity here because the endpoints don’t work, so why not choose the next best option (midpoint) if it helps prove your point. We have confirmed that a “random” rectangle already has area greater than 37, so surely it’s not far fetched to argue that the maximum area of the trapezoid will have more area than that. In fact, this works as a proof as well and you didn’t have to do all the aforementioned things even in a “math class”. After all, our whole agenda is to show that the area of the trapezoid is greater than 37 and not actually compute the value.
This would hold true if you do not use rectangle approach to confirm the theory and find area of trapezoid as a whole. If you set B at the point where trapezoid is maximum, the rectangle does not have maximum area. So in case the area of rectangle is lesser than the numerical value it is compared against, you cannot conclude anything . If you have to prove using a rectangle, you would still need to prove it at x=5, as the rectangle has max area there.
If the question compared it against say, 37.5. You’d not be able to conclude this USING RECTANGLE at any point [Including the point where trapezoid has max area] other than the midpoint.
Whysoshant, thank you for restating everything i already stated 2 messages prior lol.
lol, the selection of midpoint is indeed a maximiser for the rectangle. There is a very specific reason why we chose the midpoint and it was clearly not “random”, any other point and the logic to solve this question using rectangle fails.
Anyways I rest my case, no point .
The configuration shown is definitely not a maximizer.
There’s nothing wrong in this sentence I said. The configuration (this refers to the trapezoid while connecting the midpoints) is not the maximum. You constantly just keep bringing up disparate topics into the conversation because apparently you don’t want to concede when you’re wrong (happened like 2- 3 times now). You start talking about maximizing the area of the rectangle, which literally has nothing to do with maximizing the area of the trapezoid.
To reiterate, we found a convenient rectangle whose area was already greater than 37 so the maximum area of the trapezoid must have area greater than 37. There are a bunch of rectangles that meet this criteria, but we found the most straightforward one.
If you were genuinely interested in learning, you would realize that nearly everything has already been addressed. Right now, this feels like a pointless debate, where you’re focused on finding my mistakes even though none exist. However, if that wasn’t the intent then i guess i just misconstrued whatever’s happening here.
There is a very specific reason why we chose the midpoint and it was clearly not “random”
There’s none lol. It’s legit the next “easy point” to consider. Fortunately enough, this “random point” worked out nicely for us. If there was real intent then the maximizing process would’ve been shown (vertex of the quadratic).
Any other point and the logic to solve this question using rectangle fails.
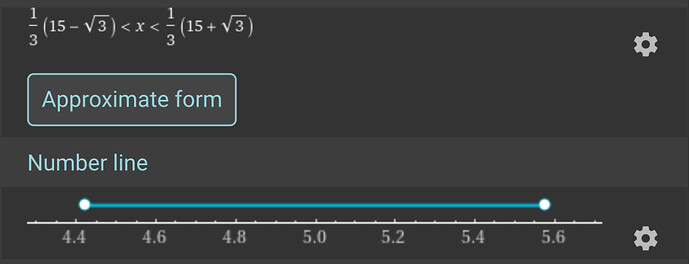
Meh, this is clearly wrong cuz any x in this range would work.
So yeah, this again validates the “random” thing lol cuz any of these values would work to prove the point.