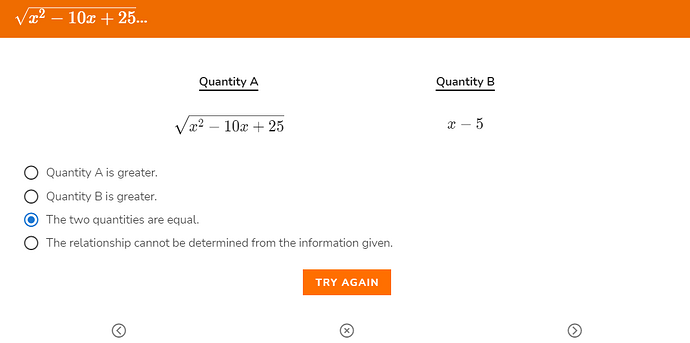
My answer was C, but it shows that is incorrect
is my answer wrong? if yes, then why?
or is the solution incorrect?
Hint: A is always positive. Does B have to be always positive?
Have you tested or all the cases ?
hint: test x = -6
I have a doubt, what if we simplify the quantity A as ((x-5)2)1/2 it comes out to be (x-5), so both quantities are equal.
Please correct me if I am wrong because this was my first approach to the problem.
That is true as long as x - 5 ≥ 0. Because when x < 5, quantity A reduces to (5 - x) and not (x - 5).
(x^2 -10x + 25) reduces to (x-5)^2 also (5-x)^2 -----Both are same : \
Think about it this way: Quantity A is \sqrt{x^2 - 10x + 25}. This, as you said, can be written as \sqrt{(x - 5)^2}. When x \geq 5, \sqrt{(x - 5)^2} is indeed x - 5. But when x < 5, x - 5 is negative, and hence Quantity A becomes 5 - x instead.
That is, for x < 5, the question reduces to
Quantity A: 5 - x
Quantity B: x - 5
while for x \geq 5, we get
Quantity A: x - 5
Quantity B: x - 5
You can see how Quantity A and Quantity B are not equal in the x < 5 case.
Oh, Okay got it,
Thank you for this explanation