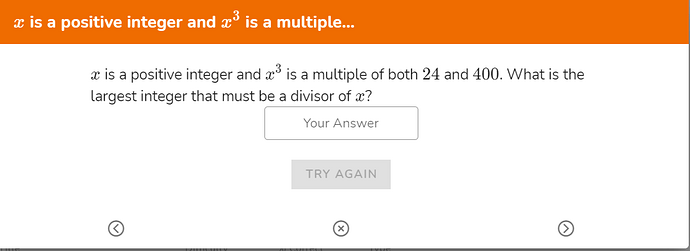
x is a positive integer and x3 is a multiple of both 2424 and 400400. What is the largest integer that must be a divisor of x?
@devanshsolani -
What is the largest integer that must be a divisor of x?
Ans- largest divisor of any number will be the number itself. Hence, x.
Now find x.
Breaking 24 and 400 in prime factorization-
24= 3*23
400= 2^4 * 52
Find a number that is multiple/divisible by both 24 and 400:
number1 = (3)(24)(52)
if we see this number1, it is not a perfect cube, but a multiple of 24 and 400.
Make the above number1 a perfect cube -as we need a cube that is multiple/divisible by 24 and 400=
x3 =number1 * 32 * 22 * 5
x3 = 33 * 26 * 53
Now, find the cube root of x^3 to get x
x= 3 * 22 * 5 = 3 * 4 * 5 = 60
Hope this helps!! 
1 Like