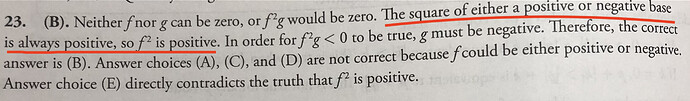So…I basically have a complete mental breakdown over the following, very simple mathematical rule:
(-x)^2 = (-x)(-x) = x^2 or (-1)^2(x)^2 …the squared goes to what’s directly in front it. Since there are parentheses it goes to everything in the parentheses.
-x^2 = -(x^2) so it remains -x^2 … the squared only goes to the term directly in front of it which in this case is only x
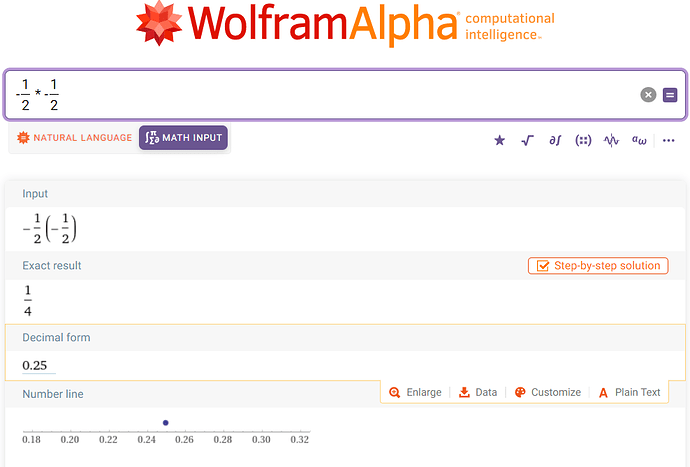
This is a very obvious rule. Greg also follows this rule in the problem shown in the screenshot. (It is from the video “Real numbers and Absolute values 1” at 1:01). → He says the square of -1/2 is -1/4.
Now my problem:
This exact rule is completely ignored in the Manhatten 5lb. Prep, as well as the ETS Prep books in some of their practice problems. Here is an example:
Here is their solution:
I am totally confused now. At a lot of problems they just give the same phrase as solution “The square of either a positive or a negative number will always be positive”, which is completely false. Can someone tell me how the real GRE handles these kinds of problems? What is “right” and what is “wrong” in the Gre? Are all squared numbers positive for the Gre??
Thank you very much in advance!