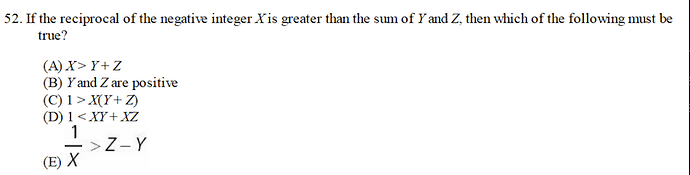Hi, I have some difficulty to trying to reach the same understanding with some of the given answers. Btw, this example is from the chapter inequality under Lb5
I couldn’t understand why
For (A), that if X = -1, it could be true?
Likewise, for (B), feels the answer is contradicting? If Y and Z are already positive, why would Y or Z a negative?
Also why would (E) could be true? I thought it is false?
The other answers are okay. I can follow the reasoning.
Thank you.
What we are given is
\frac{1}{X}>Y+Z
Now, for (A), if we have X=-1, then
\frac{1}{X}>Y+Z
becomes
\frac{1}{-1}>Y+Z
or equivalently,
-1>Y+Z
So, since we know that this inequality is true for sure, we know that and number greater than or equal to -1 will be greater that Y+Z.
And for X>Y+Z, we are comparing X=-1 to Y+Z, which we already know that Y+Z is always less than -1, and hence X=-1 is greater than Y+Z.
If this confused you, just think of what you are given, that \frac{1}{X}=\frac{1}{-1}=-1>Y+Z, and what can you conclude from that.
How to find that the case of X=-1 satisfies the new inequality? Well, you can think that X and \frac{1}{X} are equal for X equal 1 or -1, so if \frac{1}{X} is greater than Y+Z, then so is the value X since \frac{1}{X}=X. And since we know that X<0, we exclude the case of X=1.
\textbf{EXTRA:}
Indeed, we can find more numbers than -1 that satisfy both inequalities.
To have X>Y+Z given that \frac{1}{X}>Y+Z, we should require that
X\ge\frac{1}{X}>Y+Z
(If this does not make sense to you, think if we have 5>a+b then to find another number that is greater than a+b, we should require it to be greater than or equal 5).
So, we need
X\ge\frac{1}{X}
Multiplying both sides by X while keeping in mind that X<0, we get
X^2<1\qquad(*)
Thus, for any negative X that satisfies (*), we get that both X and \frac{1}{X} are greater than Y+Z. You can try taking X=-\frac{1}{2} for example!
For (B), I agree with you.
If both Y and Z are positive, then Y+Z is positive, which is never less than the negative number \frac{1}{X}.
Unless, they did not mean \text{both} Y and Z somehow, but I don’t see how that wouldn’t mean both.
They say that it is not a correct rephrasing of the original inequality, which is 100% true, both inequalities are not equivalent.
Buuuuut, the second inequality would be true if Y\ge0.
To see this, we know that \frac{1}{X} is greater than Z plus some value Y. Now, if we subtracted 2Y from Z+Y to get to Z-Y, we would get a number less than Z+Y if Y is positive. And since Z+Y is less than \frac{1}{X} and Z-Y is even smaller, we can conclude that Z-Y is smaller than \frac{1}{X}, i.e.
\frac{1}{X}>Z-Y
If we have that Y is negative, then subtracting 2Y to get from the first inequality to the second would have us increasing the number on the right hand side rather than decreasing it, and if $\frac{1}{X}>Y+Z but Z-Y>Y+Z, we can never conclude which is bigger \frac{1}{X} or Z-Y.
\textbf{EXTRA:}
How did we know that Y must be nonpositive? We can either do it by intuition, saying that if we want to get a number smaller than \frac{1}{X} given that Y+Z is smaller than \frac{1}{X}, then we should decrease the number on the right.
Or, following the same logic in the \textbf{EXTRA} part of (A), for Z-Y to be less than \frac{1}{X}, we need it to be less than or equal to Y+Z, i.e.
Z-Y\le Y+Z
0\le2Y
Which is true for non-negative Y.
