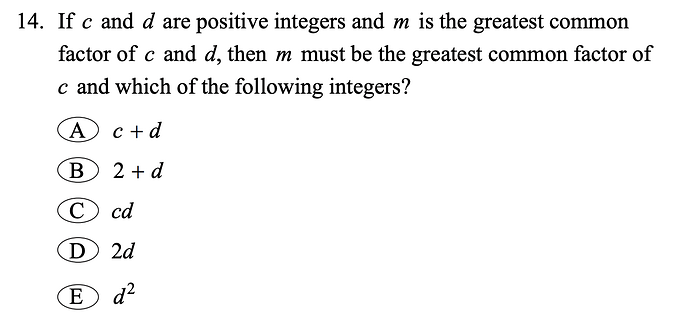Is There a Faster Way to Solve This GCF Problem?

[user3197]

My Question:

Is there a quicker or more intuitive way to solve this problem without testing each option? Any tips for approaching such questions under timed conditions?

My Solution:

1. c+d:
   m divides c and d, so it must divide c+d. Therefore, mmm is the GCF of c and c+d.
2. Other options (c+2d, d+2c, cd, 2d, d^2):
   While mmm may divide these expressions, it is not guaranteed to remain the GCF of ccc and these values. For example:

• GCF(c,c+2d) could be larger than mmm.
• GCF(c,cd) is c, not m.

Final Answer:

The only guaranteed expression is:

c+d​

[cylverixxx]

I mean since it’s a multiple-choice question then it’s very easy to test numbers tbh.

Anyway, yeah \operatorname{gcd} (c, d) = \operatorname{gcd} (c, d + cn) (for some integer n) and you can prove this via bezout.