Largest right cylinder inside rectangular box

[user4528]

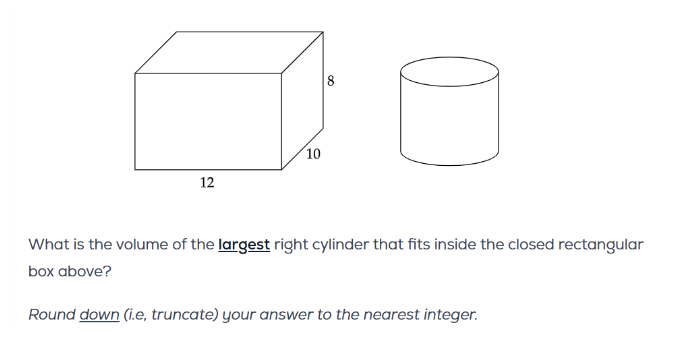
I am confused as to how identify the dimensions of the rectangular box when they don’t explicitly tell which one is width, height and length. For reference, consider this first question:

It’s clear that the height is 8, which will also be the height of the cylinder, and that the radius should fit either if we use the length or width. Since width is smaller and equal to 10, largest radius is 5 and the volume is pir^2h, approx 628. No problem.

But consider this second exercise where they just give the dimensions of the rectangular box and we don’t know for sure which one is height, length of width. My reasoning was that we’d need to treat it as a cube of 8x8x8, in which case h=8 and r=4. But Greg says that the height is 8 and that the radius is 5 (so as to fit in the side of 10 inches). How can you be sure that the height is 8?

Note that since the r is squared in the volume of a cylinder this is not an irrelevant point. Assuming one or another as the height leads to different volumes.

[cylverixxx]

Conventionally, the dimensions of the box would be interpreted as (l,w,h) = (8,10,12) – if the assignment order is a source of confusion. Regardless, the specific order shouldn’t matter when attempting to maximize the volume of said cylinder.

We have a rectangular box with three distinct face dimensions: (8 \times 10), (8 \times 12), and (10 \times 12). It should hopefully be obvious that the (10 \times 12) face allows for the largest possible cylinder radius (and consequently the maximum volume too). Owing to the properties of a circle, we designate the 10 dimension as the diameter of the circle. Finally, as the only remaining dimension is 8, this must be the height of the cylinder.